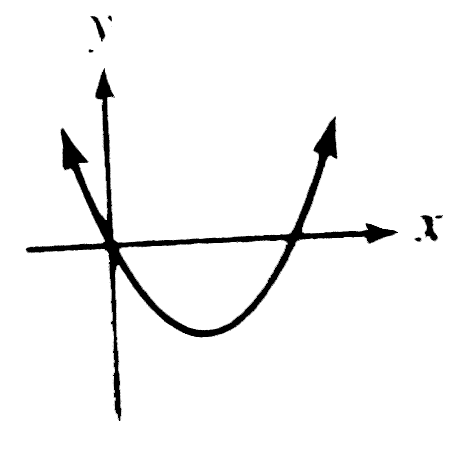
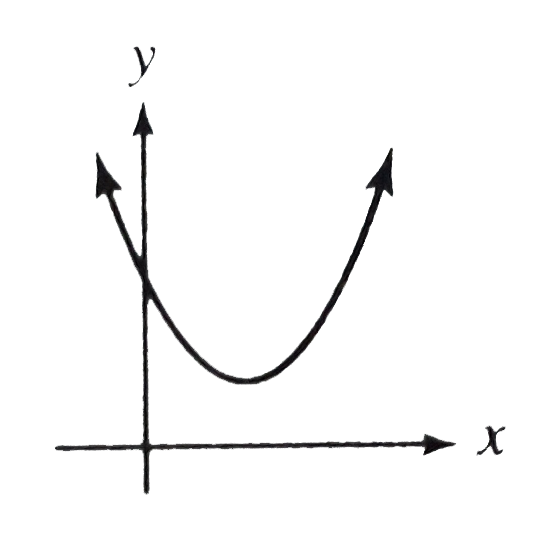
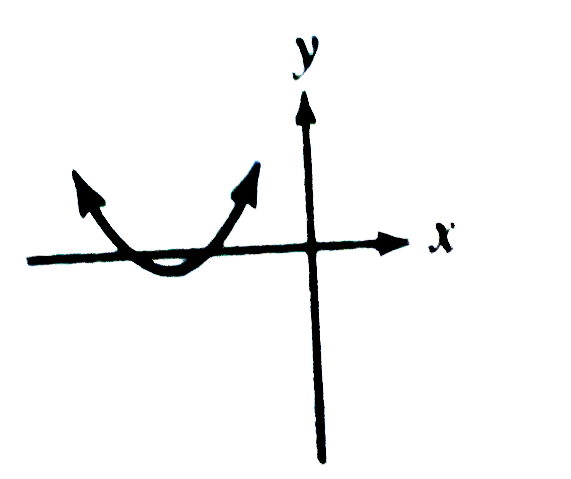
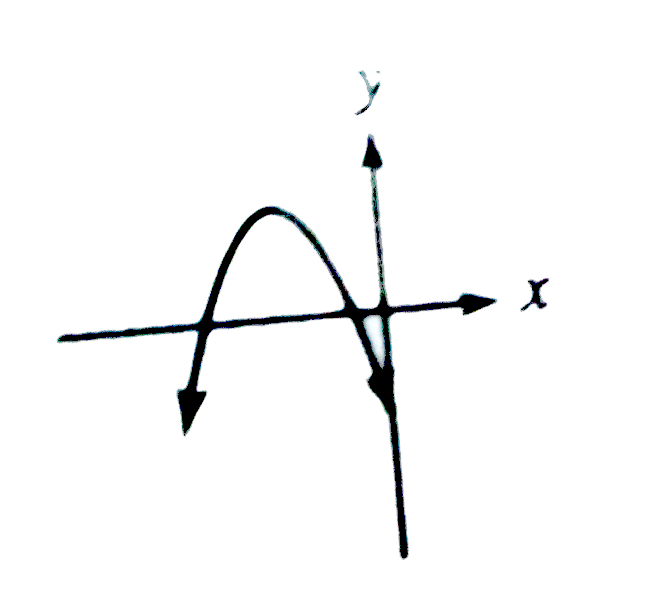
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which could be the graph of y=x^2 + 3x+k , where k is an integer ?
Text Solution
|
- Find the area in the 1* quadrant bounded by [x]+[y]=n, where n in N an...
Text Solution
|
- The graph of curve x^(2)=3x-y-2 is strictly below the line y=k ,then-
Text Solution
|
- lim(x rarr k)(x-[x]), where k is an integer,is equal to (where denotes...
Text Solution
|
- If the area bounded by the curve |y|=e^(-|x|)-(1)/(2) and (|x|+|y|)/(2...
Text Solution
|
- If (x+p) is a factor of both x^(2)+16x+64 and 4x^(2)+37x+k, where p an...
Text Solution
|
- If f(x)=3x^(2)+4x+5, what must the value of k equal so that the graph ...
Text Solution
|
- Which of the following translations of the graph of y = x^(2) would re...
Text Solution
|
- If g(x)=-2 intersects the graph of y=f(x)+k at one point, which of the...
Text Solution
|