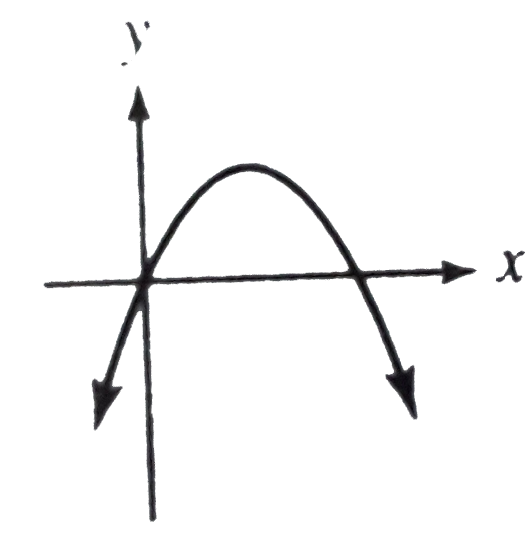
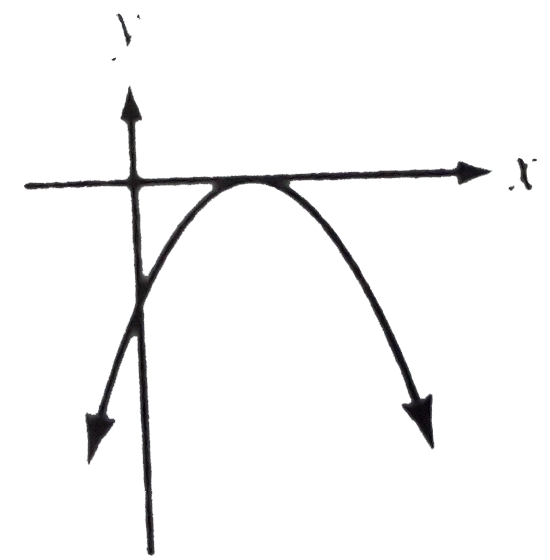
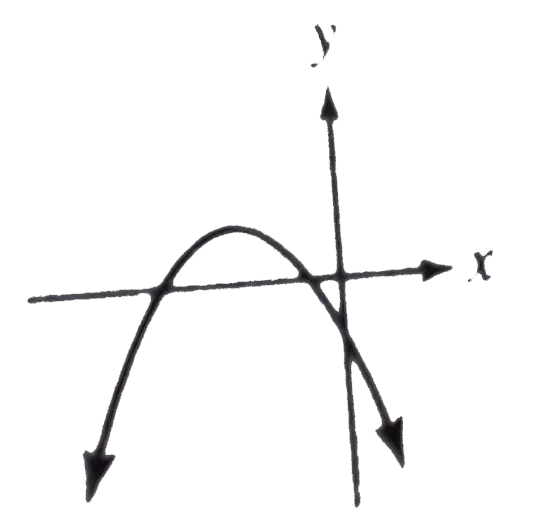
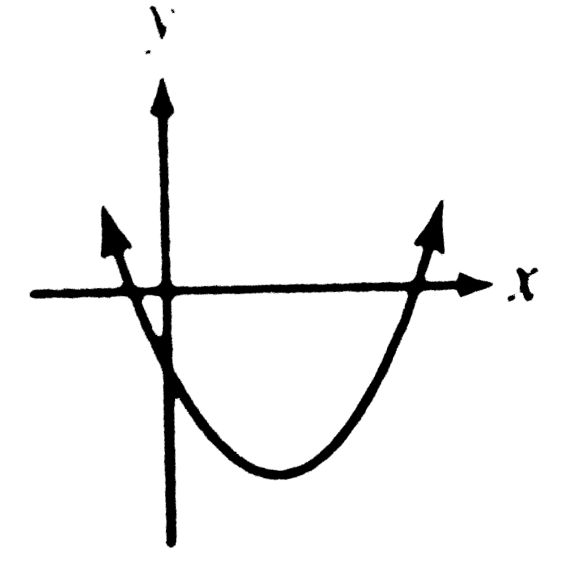
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If f(x)=ax^2 + bx + c , a ne 0 and a, b , and c are all negative , whi...
Text Solution
|
- Let f(x)=ax^2-bx+c^2 != 0 and f(x) != 0 for all x in R. Then (a) a^2+c...
Text Solution
|
- which of the following graph represents the expression f(x) = ax^2 + b...
Text Solution
|
- Consider the quadratic function f(x)=ax^(2)+bx+c where a,b,c in R and ...
Text Solution
|
- Let f(x) = ax^(2) - bx + c^(2), b ne 0 and f(x) ne 0 for all x in R. T...
Text Solution
|
- For which of the following graphs of the quadratic expression f(x)=ax^...
Text Solution
|
- If f(x) =ax^(2) +bx + c, g(x)= -ax^(2) + bx +c " where " ac ne 0 "...
Text Solution
|
- If in the quadratic function f(x)=ax^(2)+bx+c, a and c are both negati...
Text Solution
|
- If f(x)=ax^2 + bx + c , a ne 0 and a, b , and c are all negative , whi...
Text Solution
|