A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
IMPROVING YOUR MATH SCORE
ENGLISH SAT|Exercise BASIC MATH PROBLEMS IN SETTINGS|6 VideosIMPROVING YOUR MATH SCORE
ENGLISH SAT|Exercise VERY CHALLENGING PROBLEMS|12 VideosHIGHER DEGREE POLYNOMIALS
ENGLISH SAT|Exercise EXERCISES|6 VideosINTERMEDIATE ALGEBRA/COORDINATE GEOMETRY
ENGLISH SAT|Exercise EXERCISE|12 Videos
Similar Questions
Explore conceptually related problems
ENGLISH SAT-IMPROVING YOUR MATH SCORE-VERY CHALLENGING PROBLEMS
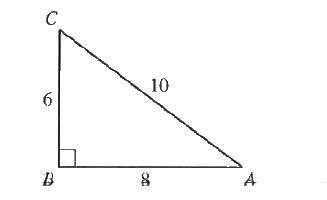
- What is the sine of /A in the triangle below?
Text Solution
|
- If 537^(102) were calculated, it would have 279 digits. What would the...
Text Solution
|
- If a < -1, which of the following best descirbes a general relationshi...
Text Solution
|
- If (4/5)^(n) = sqrt((5/4)^(3)), then n = ?
Text Solution
|
- In the standard (x,y) coordinate plane, the triangle with vertices at ...
Text Solution
|
- In the figure below, bar(AB) -= bar(AC) and bar(BC) is 10 units long. ...
Text Solution
|
- A bag of pennies could be divided among 6 children, or 7 children, or ...
Text Solution
|
- There are n students in a class. If, among those students, p% play at ...
Text Solution
|
- Starting at her doorstip, Ramona walked down the sidewald at 1.5 feet ...
Text Solution
|
- An object detected or radar is 5 miles to the east, 4 miles to the nor...
Text Solution
|
- At both Quick Car Rental and Speedy Car Rental, the cost, in dollars, ...
Text Solution
|
- At both Quick Car Rental and Speedy Car Rental, the cost, in dollars, ...
Text Solution
|
- At both Quick Car Rental and Speedy Car Rental, the cost, in dollars, ...
Text Solution
|