A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
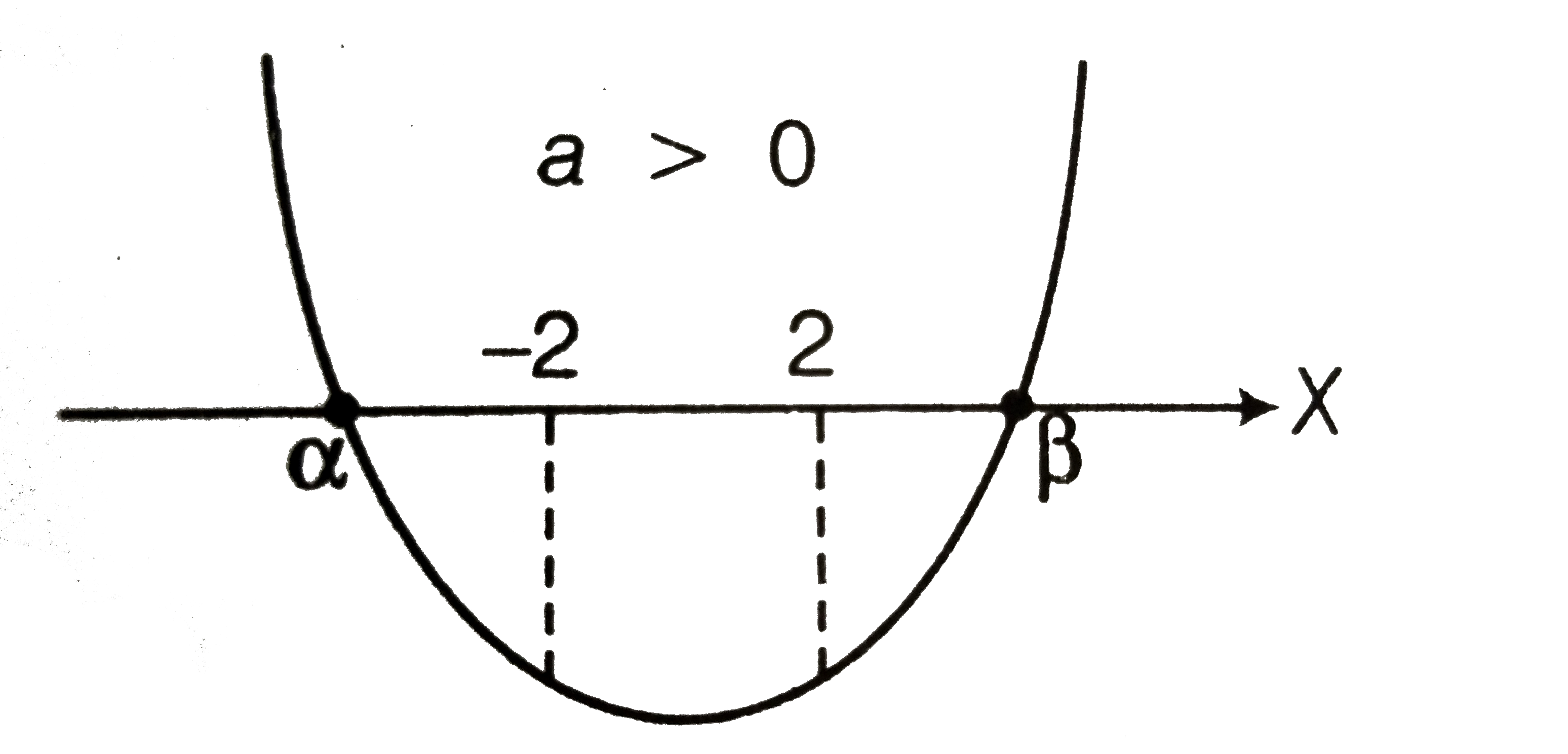
- ax^2 + bx + c = 0(a > 0), has two roots alpha and beta such alpha < -2...
Text Solution
|
- If alpha and beta be the roots of the equation ax^(2)+bx+c=0 then equa...
Text Solution
|
- If alpha,beta are roots of the equation ax^(2)-bx-c=0, then alpha^(2)-...
Text Solution
|
- If alpha,beta are the roots of ax^(2)+bx+c-0 then alpha beta^(2)+alpha...
Text Solution
|
- If alpha,beta are the roots of ax^(2)+bx+c=0 then the value ((alpha)/(...
Text Solution
|
- Two roots of the equation ax^2 +bx +c=0 is alpha,beta then find the va...
Text Solution
|
- If the equation ax^2 + bx + c = 0 ( a gt 0) has two roots alpha and be...
Text Solution
|
- If alpha , beta are the roots of ax^2 + bx + c=0 then alpha beta ^(2) ...
Text Solution
|
- IF alpha , beta are the roots of ax ^2 + bx +c=0 then (alpha ^2...
Text Solution
|