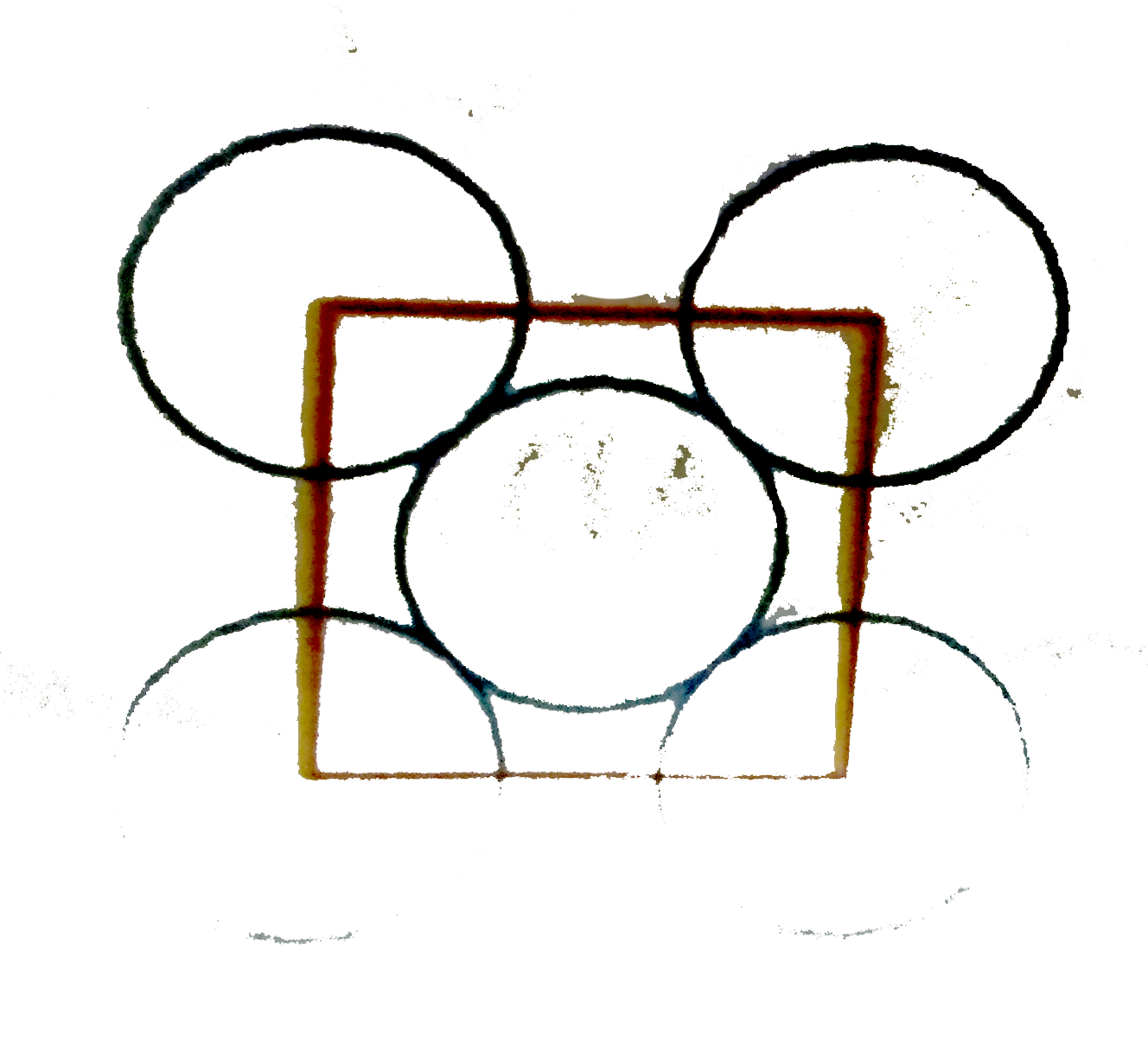Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Metal M of radius 50 nm is crystallized in fcc type and made cubical c...
Text Solution
|
- Metal M of radius 50 nm is crystallized in fcc type and made cubical c...
Text Solution
|
- What is the number of atoms in a unit cell of face-centred cubic cryst...
Text Solution
|
- In a face-centred cubic crystal, the neighbour distance is …… times th...
Text Solution
|
- In a face-centred cubic crystal, the nearest neighbour distance is ti...
Text Solution
|
- A cubic crystal has "" faces.
Text Solution
|
- A metal crystallizes into two cubic systems - face centred cubic (fcc)...
Text Solution
|
- एक धातु फलक केन्द्रित घंन व्यवस्था में क्रिस्टलीकृत है। यदि इसकी मात्र...
Text Solution
|
- The packing fraction in a face - centred cubic cell of crystals is
Text Solution
|