Home
Class 12
PHYSICS
Two balls are thrown simultaneously, A v...

Two balls are thrown simultaneously, A vetically upwards with a speed of `20 ms^(-1)` from the ground, and B vetically downwards from height of 40 m with the same speed and along the same line of motion. At what points do the two balls collide? Take `g= 9.8 ms^(-2)`.

Text Solution

Verified by Experts

Suppose the two balls meet at a height of x from the ground after time t s from the start. For upward motion of balls A :
`u=20ms^(-1),g=9.8ms^(-2)`
`s=ut+1/2"gt"^2`
`x=20t-1/2xx9.8t^2=20t-4.9t^2`

For downward motion of ball B
`40-x=20xxt+1/2xx9.8t^2`
`=20t+4.9t^2`
Adding (i) and (ii) 40=40 or t=1s
From (i), x=`20xx1-49xx(1)^2=15.1m`
Hence the two balls will collide after 1 s at a height of 15.1 m from the ground.
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    MOTION|Exercise EXERCISE 1 OBJECTIVE PROBLEMS|103 Videos

  • KINEMATICS

    MOTION|Exercise EXERCISE 2 OBJECTIVE PROBLEMS|75 Videos

  • HYDROSTATIC, FLUID MECHANICS & VISCOSITY

    MOTION|Exercise EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM|7 Videos

  • KINETIC THEORY OF GASES

    MOTION|Exercise EXERCISE-3 SECTION-B|16 Videos

Similar Questions

Explore conceptually related problems

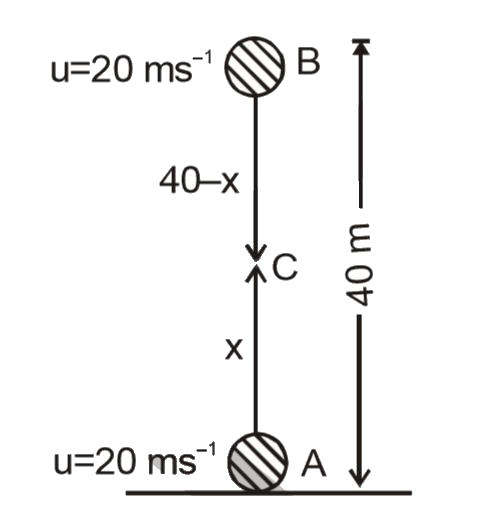
Two balls are thrown simultaneously, A vertically upwards with a speed of 20 m/s from the ground, and B vertically downwards from a height of 40 m with the same speed along the same line of motion. At what point do the two balls collide? Take g = 9.8 m//s^(2) .

A ball 'A' is thrown upwards from ground level with a velocity of 20 ms^(-1) . Another ball 'B' is thrown downwards from a height of 40 m with the same speed. Find the height at which the two balls meet (take g = 10 m s^(-2) ).

A ball is thrown vertically upwards with a speed of 9.8 m/s from the ground. Draw the x-t, v-t and a-t graph for its motion.

A ball thrown vertically upwards with a speed of 19.6 ms^(-1) from the top of a tower returns to earth in 6 s . Calculate the height of the tower.

Two balls of different masses are thrown vertically upwards with the same speed . They pass through the point of projection in their downward motion with the same speed ( Neglect air resistance ).

A ball is thrown vertically upward with speed 40 m//s . Simultaneously, another ball is dropped from a height 200 m in the same verticle line. When and where the balls meet?

Two balls are projected vertically upward with same speed 35 m/s in 3s interval. Find height at which both balls collide.

A ball is thrown vertically upwards with a velocity of 20 ms^(-1) from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground. How long will it be before the ball hits the ground (Take, g=10 ms^(-2) ) ?

A ball is thrown vartically upward with speed 70 m//s . After 1 s, another ball is dropped from a height 185 m in the same vertical line. When and where the balls collide?