Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-WORK, POWER & ENERGY -Exercise - 3 Section-B
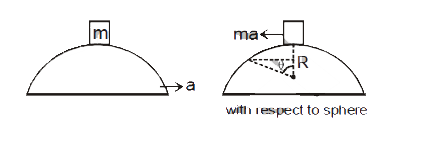
- A smooth spehre of radius R is made to translate oin a straight line w...
Text Solution
|
- A body of mass m is acceleratad uniformaly from rest to a speed v in a...
Text Solution
|
- A spherical ball of mass 20kg is stationary at the top of a hill of he...
Text Solution
|
- A body A of mass M while falling wertically downwards under gravity br...
Text Solution
|
- The block of mass M moving on the frictionless horizontal surface col...
Text Solution
|
- A mass ‘m’ moves with a velocity ‘v’ and collides inelastically with a...
Text Solution
|
- A mass of M kg is suspended by a weightless string. The horizontal for...
Text Solution
|
- A particle of mass 100 g is thrown vertically upwards with a speed of ...
Text Solution
|
- A ball of mass 0.2 kg is thrown vertically upwards by applying a force...
Text Solution
|
- The potential energy of a 1 kg particle free to move along the x- axis...
Text Solution
|
- A bomb of mass 16kg at rest explodes into two pieces of masses 4 kg an...
Text Solution
|
- Consider a two particle system with particles having masses m1 and m2 ...
Text Solution
|
- A 2kg block slides on a horizontal floor with the a speed of 4m//s it ...
Text Solution
|
- As athlete in the olympic ganes cover a distance of 100 m in 10 s. Hi...
Text Solution
|
- A block of mass 0.50kg is moving with a speed of 2.00m//s on a smooth ...
Text Solution
|
- Statement -1: Two particles moving in the same direction do not lose a...
Text Solution
|
- A particle is moving with velocity vecv = k( y hat(i) + x hat(j)) , w...
Text Solution
|
- At time t=0s particle starts moving along the x- axis. If its kinetic ...
Text Solution
|
- This question has statement I and statement II. Of the four choices gi...
Text Solution
|
- When a rubber bandis streched by a distance x , if exerts resuring fop...
Text Solution
|
- A person trying to lose weight by burning fat lifts a mass of 10 kg up...
Text Solution
|