Home
Class 11
MATHS
lim(xrarrpi/2)tanx...

`lim_(xrarrpi/2)tanx`

Promotional Banner

Topper's Solved these Questions

  • DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY

    SURA PUBLICATION|Exercise EXERCISE 9.2|14 Videos

  • DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY

    SURA PUBLICATION|Exercise EXERCISE 9.3|12 Videos

  • COMBINATORICS AND MATHEMATICAL INDUCTION

    SURA PUBLICATION|Exercise ADDITIONAL PROBLEMS (section - D)|5 Videos

  • DIFFERENTIAL CALCUS - DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION

    SURA PUBLICATION|Exercise ADDITIONAL PROBLEMS SECTION-D (5 MARKS)|4 Videos

Similar Questions

Explore conceptually related problems

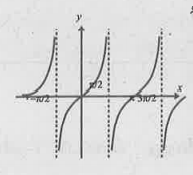
Use the graph to find the limits (if it exists).If the limit does not exist ,explain why? lim_[xrarr(pi/2)]tanx

The value of lim_(xrarrpi//4) (tan^(3)x-tanx)/(cos(x+(pi)/(4))) is

If f(x)=(cosx)/((1-sinx)^(1/3)) then (a) ("lim")_(xrarrpi/2)f(x)=-oo (b) ("lim")_(xrarrpi/2)f(x)=oo (c) ("lim")_(xrarrpi/2)f(x)=o (d) none of these

lim_(xrarr(pi)/(2)) (1-sinx)tanx=

Find (a) lim_(xrarr0)tanx/|x|

lim_(xrarr0) (3 tan3x-4 tan2x-tanx)/(4x^(2)tanx)

Evaluate the following limits in lim_(xrarrpi)(sin(pi-x))/(pi(pi-x))

Evaluate : lim_(xrarr0)(tanx)/(x)

Lim_(x rarr 0)(tanx sqrt (tanx)-sin x sqrt(sinx))/(x^(3).sqrtx) equals