Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-TRIANGLES -EXERCISE 2.6 (OPTIONAL)
- In Fig PS is the bisector of angleQPR " of " DeltaPQR . Prove that (...
Text Solution
|
- In Fig . D is a point on hypotenuse AC of DeltaABC, bot DM botBCand DN...
Text Solution
|
- In Fig . D is a point on hypotenuse AC of DeltaABC, bot DM botBCand DN...
Text Solution
|
- In Fig , ABC is a triangle in which angleABCgt90^(@) and AD bot CB, ...
Text Solution
|
- In Fig . ABC is a triangle in which angleABClt90^(@)and AD botBC. P...
Text Solution
|
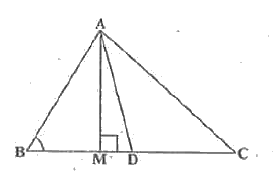
- In Fig . AD is a median of a triangle ABD and AM bot BC. Prove that...
Text Solution
|
- In Fig . AD is a median of a triangle ABD and AM bot BC. Prove that...
Text Solution
|
- In Fig . AD is a median of a triangle ABD and AM bot BC. Prove that...
Text Solution
|
- If the diagonals of a parallelogram are equal, show that it is a recta...
Text Solution
|
- In Fig . two chords AB and CD intersect each other at the point P. pro...
Text Solution
|
- In Fig . two chords AB and CD intersect each other at the point P. pro...
Text Solution
|
- In Fig. two chords AB and CD of a circle intersect each other at the ...
Text Solution
|
- In Fig. two chords AB and CD of a circle intersect each other at the ...
Text Solution
|
- In Fig .D is a point on side BC ofDeltaABC such that (BD)/(CD) =(AB)/...
Text Solution
|
- A conical tent is 10 m high and the radius of its base is 24 m. Find ...
Text Solution
|