Home
Class 9
MATHS
In a triangle ABC, E is the mid-point of...

In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = `(1)/(4)` ar (ABC).

Text Solution

Verified by Experts

The correct Answer is:
`(1)/(4)` ar (ABC).
Promotional Banner

Topper's Solved these Questions

  • AREA OF PARALLELOGRAMS AND TRIANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 11.4|3 Videos

  • AREA OF PARALLELOGRAMS AND TRIANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 11.2|6 Videos

  • APPENDIX A

    SUBHASH PUBLICATION|Exercise EXERCISE A 1.4|10 Videos

  • CIRCLES

    SUBHASH PUBLICATION|Exercise EXERCISE 12.6|7 Videos

Similar Questions

Explore conceptually related problems

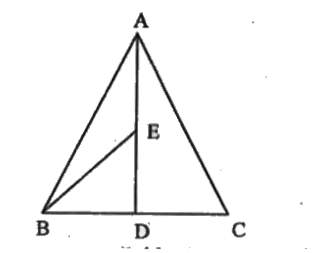
In the figure 11.23, E is any point on median AD of a Delta ABC. Show that ar (ABE) = ar (ACE).

In the Given figure, E is any point on median AD of a triangle ABC Show that ar (ABE) = ar (ACE)

If E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = (1)/(2) ar (ABCD)

In P is a point in the interior of a parallelogram ABCD. Show that (ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)

In Delta ABC , AD is the median and PQ || BC . Prove that PE = EQ

In, PQRS and ABRS are parallelograms and X is any point on side BR. Show that ar (PQRS) = ar (ABRS) as (AXS) = (1)/(2) ar (PQRS)

In, D and E are two points on BC such that BD = De = EC. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the 'introduction' of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?

IN the figure, P is a point in the interior of a parallelogram ABCD. Show that (i) ar(APB) + ar(PCD) = 1/2 ar (ABCD) (ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)