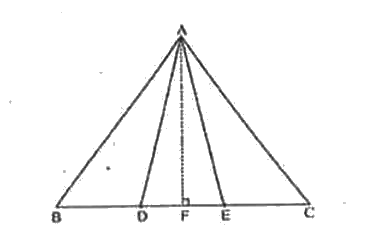
In, D and E are two points on BC such that BD = De = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the 'introduction' of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?