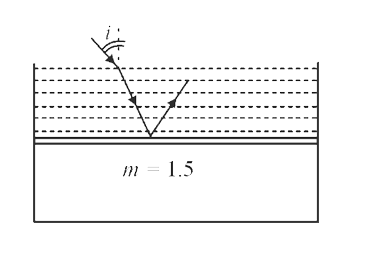
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider a tank made of glass (refractive index 1.5) with a thick bott...
Text Solution
|
- Consider a tank made of glass (refractive index 1.5) with a thick bott...
Text Solution
|
- mu अपवर्तनांक वाले काँच की समतल सतह पर एक प्रकाश कोण i पर आपतित होता...
Text Solution
|
- वह आपतन कोण जिस पर परावर्तित प्रकाश वायु से काँच (अपवर्तनांक n) में पर...
Text Solution
|
- Consider a tank made of glass (refractive index 1.5) with a thick bott...
Text Solution
|
- हवा से काँच परावर्तन के लिए आपतन कोण का वह मान जिसके लिए परावर्तित प्र...
Text Solution
|
- If a small angled prism, made of glass is immersed in a liquid of refr...
Text Solution
|
- प्रकाश की समांतर बीम, किसी समतल काँच की सतह पर 60^(@) के कोण पर आपतित ...
Text Solution
|
- काँच (अपवर्तनांक =1.5) से बने एक टैंक की तली मोटी है | इसमें अपवर्तना...
Text Solution
|