Home
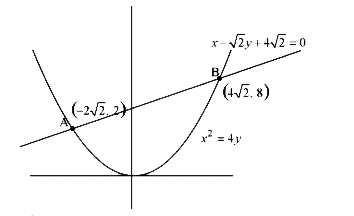
Class 12
MATHS
The length of the chord of the parabola ...

The length of the chord of the parabola `x^(2) = 4y` having equations `x - sqrt(2) y + 4 sqrt(2) = 0` is

A

`8sqrt(2)`

B

`2sqrt(11)`

C

`6sqrt(3)`

D

`3sqrt(2)`

Text Solution

Verified by Experts

The correct Answer is:
C

`x^(2)=4y .....(i)`
`x-sqrt(2)y+4sqrt(2)=0`
`x=sqrt(2)y-4sqrt(2).......(ii)`
For Point of intersection we will solve both the equation
`(sqrt(2)y-4sqrt(2))^(2)=4y`
`2y^(2)+32-16y=4y`
`y^(2)-10y+16=0`
`y^(2)-2y-8y+16=0`
`(y-2)(y-8)=0`
`y=2, y=8`
`x^(2)=8`
`x=pm 2sqrt(2)`
`A=-2sqrt(2),2)`
`x^(2)=32`
`x=pm 4sqrt(2)`
`B(4 sqrt(2),8)`
`"(dist)"_(AB)=sqrt((4sqrt(2)-(-2sqrt(2)))^(2)+(8-2)^(2))`
`=sqrt(36xx2+36)`
dist `=6sqrt(3)`
Promotional Banner

Similar Questions

Explore conceptually related problems

The length of the chord 4y=3x+8 of the parabola y^(2)=8x is

The length of the chord of the parabola y^(2)=4ax whose equation is y-x sqrt2+4asqrt2=0 is

Find the length of the chord of the parabola y^(2)=8x, whose equation is x+y=1

The length of the common chord of the parabolas y^(2)=x and x^(2)=y is

The mid-point of the chord 2x+y-4=0 of the parabola y^(2)=4x is

The chord of the parabola y^(2)=4ax, whose equation is y-x sqrt(2)+4a sqrt(2)=0, is a normal to the curve,and its length is sqrt(3)a then find lambda.

The length of the chord of the parabola y^(2)=x which is bisected at the point (2,1) is (a) 2sqrt(3)( b) 4sqrt(3)(c)3sqrt(2) (d) 2sqrt(5)

The length of the chord of the parabola x^(2) = 4y passing through the vertex and having slope cot alpha is

The length of the chord of the parabola x^(2) = 4 y passing through the vertex and having slops cot alpha is