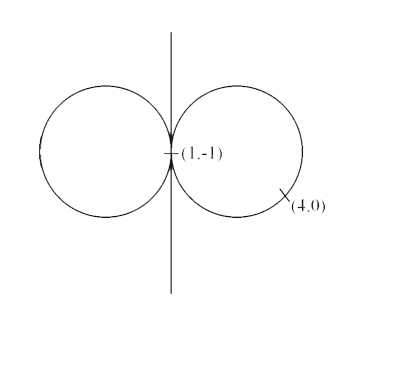A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- lf a circle C passing through (4,0) touches the circle x^2 + y^2 + 4x-...
Text Solution
|
- If a circle C passing through (4,0) touches the circle x^(2)+y^(2)+4x-...
Text Solution
|
- If circle C passing through the point (2, 2) touches the circle x^2 +...
Text Solution
|
- Centre of the circle whose radius is 3 and which touches internally th...
Text Solution
|
- If a circle C passing through the point (4,0) touches the circle x^(2)...
Text Solution
|
- The equation of the circle passing through the points of intersectio...
Text Solution
|
- The equation of the circle passing through the points of intersection ...
Text Solution
|
- एक वृत्त C, बिंदु (4,0) से होकर जाता है तथा वृत्त x^(2) + y^(2) + 4x-6...
Text Solution
|
- The equation of the circle whose radius is 3 and which touches interna...
Text Solution
|