Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
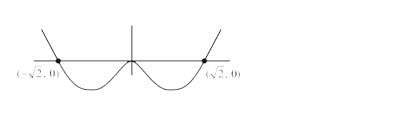
- Let I=int(a)^(b)(x^(4)-2x^(2))dx. If I is minimum then the ordered pai...
Text Solution
|
- If IK=int1^e(lnx)^kdx(k in I^+)dx(k in I^+), then find the value of...
Text Solution
|
- Let I=int(1)^(3)|(x-1)(x-2)(x-3)|dx. The value of I^(-1) .
Text Solution
|
- Let I=int(1)^(3)|(x-1)(x-2)(x-3)|dx The value of I^(-1) .
Text Solution
|
- Let I (a) =int(0)^(pi) ((x)/(a)+ a sin x)^(2) dx, where 'a' is positiv...
Text Solution
|
- Let I=int(a)^(b)(x^(4)-2x^(2))dx. If I is minimum then the ordered pai...
Text Solution
|
- I=int(0)^(4)(x^(2)+2x+4)dx
Text Solution
|
- Let I=int(a)^(b)(x^(4)-2x^(2))dx. If I is minimum then the ordered pai...
Text Solution
|
- If int(x^(2)+2x^(4)+3x^(6))(1+x^(2)+x^(4))^(1/2)dx=k(Ax^(2)+Bx^(4)+Cx^...
Text Solution
|