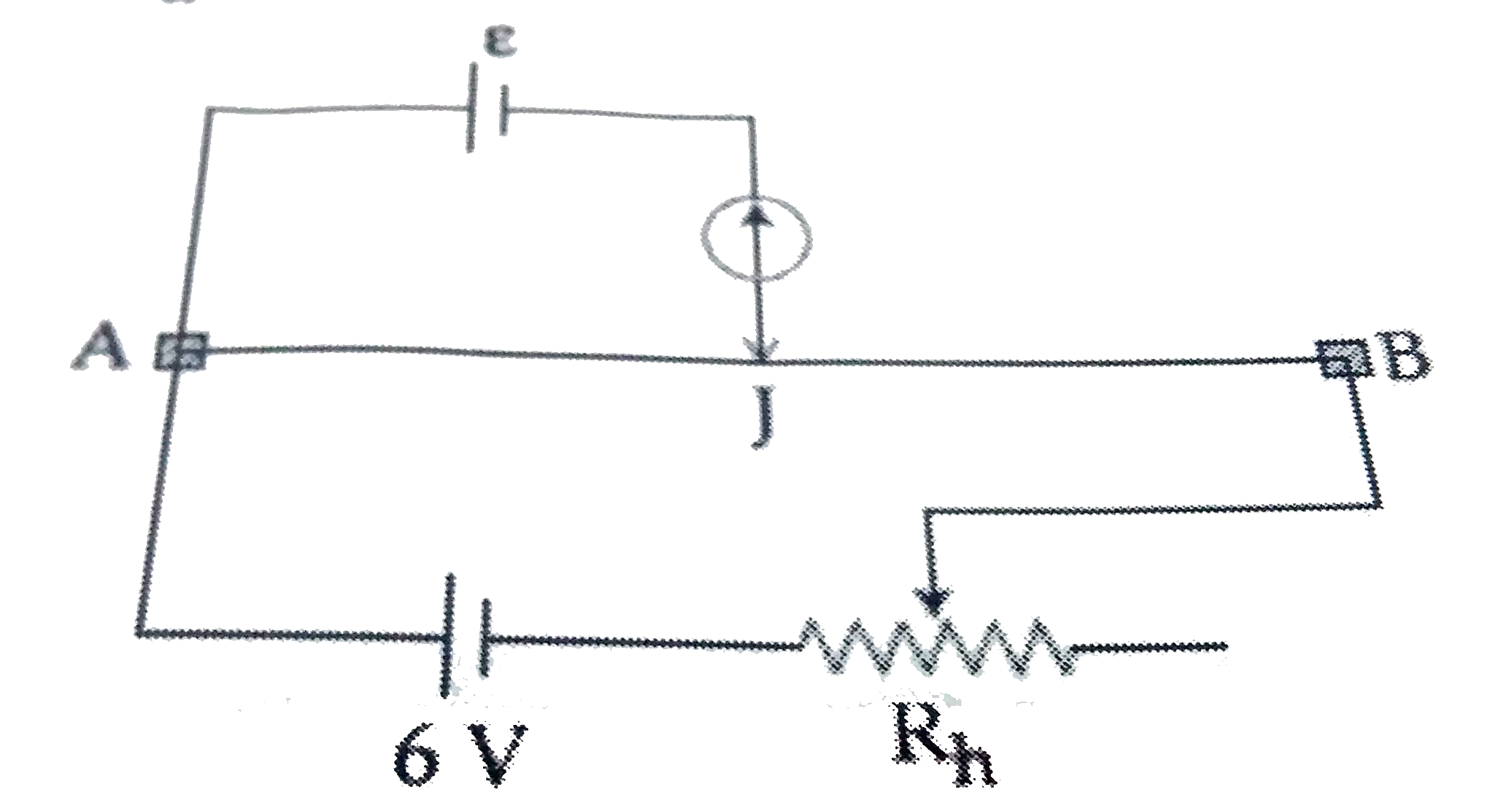
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The resistance of the meter bridge AB in given figure is 4 Omega .With...
Text Solution
|
- A cell of emf epsilon and internal resistance r gives a current of 0.5...
Text Solution
|
- A cell of emf epsilon and internal resistance r is connected across a ...
Text Solution
|
- In the circuit shown in Fig. the emf of the sources is equal to xi = ...
Text Solution
|
- In the circuit shown in the figure R(1) =3 Omega,R(2) = 2 Omega and R(...
Text Solution
|
- As shown, the circuit is made of 8 different resistance. It is found t...
Text Solution
|
- Determine the voltage drop across the resistance R(1) in the circuit g...
Text Solution
|
- The resistance of the meter bridge AB in given figure is 4 Omega .With...
Text Solution
|
- In Fig. 27-43, the current in resistance 6 is i(6)= 2.80 A the resista...
Text Solution
|