Home
Class 12
PHYSICS
Two equal resistances when connected in ...

Two equal resistances when connected in series to a battery ,consume electric power of 60 W .If these resitances are now connected in parealled combination to the same battery ,the electric power cansumed will be :

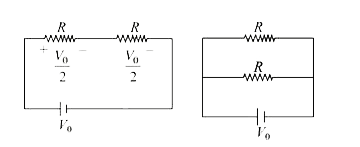
Text Solution

Verified by Experts

The correct Answer is:
B, D
`P_0=1/R(V_0/2)^2xx2=V_0^2/(2R)`
`P=V_0^2/Rxx2`
So, `P/P_0`=4
`because P_0`=60w `rArr` P = 60 x 4 = 240 w
Promotional Banner

Similar Questions

Explore conceptually related problems

Two equal resistances are connected in seires across a battery and consume a power P If these are connected in parallel, then power consumed will be

Four equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .

When three identical bulbs are connected in series. The consumed power is 10W. If they are now connected in pa rallel then the consumed power will be:-

Two electric lamps of 40 watt each are connected in parallel. The power consumed by the combination will be

When two resistances R_1 and R_2 are connected in series , they consume 12 W powers . When they are connected in parallel , they consume 50 W powers . What is the ratio of the powers of R_1 and R_2 ?

Five equal resistors when connected in series dissipated 5 W power. If they are connected in paralle, the power dissipated will be

Five equal risistors when connected in series dissipted 5 W power. If they are connected in parallel, the power dissipated will be

When galvanometer of unknown resistance connected across a series combination of two identical batteries each of 1.5 V, the current through the resistor is 1A. When it is connected across parallel combination of the same batteries, the current through it is 0.6 A. The internal resistance of each battery is

Assertion : Two identical bulbs when connected across a battery, produce a total power P. When they are connected across the same battery in series total power consumed will be (P)/(4) . Reason : In parallel, P=P_(1)+P_(2) and in series P=(P_(1)P_(2))/(P_(1)+P_(2))