Home
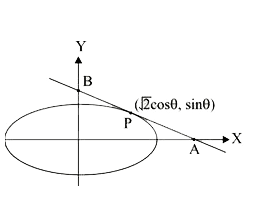
Class 12
MATHS
If tangents are drawn to the ellipse x^2...

If tangents are drawn to the ellipse `x^2+2y^2=2,` then the locus of the midpoint of the intercept made by the tangents between the coordinate axes is `1/(2x^2)+1/(4y^2)=1` (b) `1/(4x^2)+1/(2y^2)=1` `(x^2)/2+y^2=1` (d) `(x^2)/4+(y^2)/2=1`

A

`x^2/4+y^2/2=1`

B

`1/(4x^2)+1/(2y^2)=1`

C

`1/(2x^2)+1/(4y^2)=1`

D

`x^2/2+y^2/4=1`

Text Solution

Verified by Experts

The correct Answer is:
C
`x^2/2+y^2/1=1`
Let the point of contact be (`sqrt2 cos theta , sin theta`)
`therefore` Equation of tangent is `x/sqrt2 cos theta + y sin theta =1`
So, `A-=(sqrt2/(cos theta), 0)` and `B-=(0,1/(sintheta))`
Let the midpoint of AB is (h,k)
`therefore h=(sqrt2/(costheta)+0)/2rArr cos theta =1/sqrt(2h)`..(i)
and `k=(0+1/(sintheta))/2rArr sintheta=1/(2k)` ...(ii)
squaring and adding (i) and (ii) `1/(2x^2)+1/(4y^2)=1`
Promotional Banner

Similar Questions

Explore conceptually related problems

The locus of mid points of intercept made by tangents between co-ordinate axis of ellipse x^(2)+2y^(2)=2 is (A) (1)/(4x^(2))+(1)/(2y^(2))=1(B)(x^(2))/(2)+(y^(2))/(4)=1(C)(x^(2))/(4)+(y^(2))/(2)=1(D)(1)/(2x^(2))+(1)/(4y^(2))=1

Find the locus of mid-point of the portion of tangent intercepted between coordinate axes to the circle x^(2)+y^(2)=1

The least intercept made by the coordinate axes on a tangent to the ellipse (x^(2))/(64)+(y^(2))/(49)=1 is

Tangent is drawn at the point (-1,1) on the hyperbola 3x^2-4y^2+1=0 . The area bounded by the tangent and the coordinates axes is

Prove that the minimum length of the intercept made by the axes on the tangents to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 is equal to (a+b)

The locus of the foot of the perpendicular from the center of the hyperbola xy=1 on a variable tangent is (x^(2)-y^(2))=4xy(b)(x^(2)-y^(2))=(1)/(9)(x^(2)-y^(2))=(7)/(144)(d)(x^(2)-y^(2))=(1)/(16)

The locus of mid points of parts in between axes and tangents of ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 will be