A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
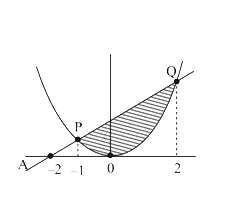
- Find the area bounded by the curve x^2=4y and the straight line x=4y-2...
Text Solution
|
- The area of the region bounded by the curve x^(2)=4y and the straight ...
Text Solution
|
- The area of the region bounded by the curve x^(2)=4y and the straight ...
Text Solution
|
- x^2 = 4y বক্র, x = 2 সরলরেখা এবং x-অক্ষ দ্বারা সীমাবদ্ধ অঞ্চলের ক্ষেত্...
Text Solution
|
- The area bonuded by the curve x^(2)=4y and the line x=4y-2 is
Text Solution
|
- The area of the region bounded by the curve x^(2)=4y and the straight ...
Text Solution
|
- The area of the region bounded by the curve x^(2)=4y and the straight ...
Text Solution
|
- Find the area bounded by the curve x^2=4y and the straight line x=4y-2...
Text Solution
|
- The area of the region bounded by the curve x^(2)=4y and the straight ...
Text Solution
|