Home
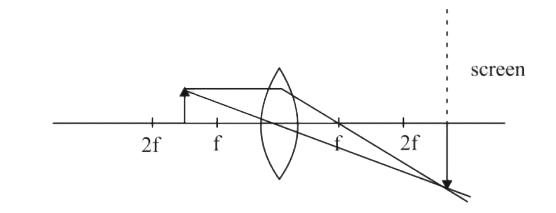
Class 12
PHYSICS
Formation of real image using a biconvex...

Formation of real image using a biconvex lens is shown below :

If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the screen ?

A

No change

B

Image disappears

C

Magnified image

D

Erect real image

Text Solution

Verified by Experts

The correct Answer is:
B
`f_("air") = f`
`(1)/(f_("m")) = ((mu_(0))/(mu_(m)) - 1) ((1)/(R_(1)) - (1)/(R_(2)))`
`(f_(m))/(f_("air")) = ((mu_(g) - 1))/(((mu_(g))/(mu_(m)) - 1)), " "f' = f(((3)/(2)-1)/((3)/((2)/(4//3)-1)))=f//12`
`f' lt f`
Hence image will not be on screen hence disappears.
Promotional Banner

Similar Questions

Explore conceptually related problems

Formation of real image using a biconves lens is shown below: If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the secreen ?

In the set up shown in Fig. will you observe interference fringes on the screen ?

A convex lens forms a real image 16 mm long on a screen. If the lens is shifted to a new position without disturbing the object or the screen then again a real image of length 81 mm is formed. The length of the object must be

A convex lens makes a real image 4 cm long on a screen. When the lens is shifted to a new position without disturbing the object, we again get a real image on the screen which is 16 cm tall. The length of the object must be

It was observed that when the distance between an object and a lens decreases, the size of the image increases. What is the nature of this lens? If you keep on decreasing the distance between the object and the lens, will you still able to obtain the image on the screen? Explain

At what distance from a biconvex lens of the focal length' f must be placed an object for the distance between the object and its real image to be minimum?

Sharp image of extended object which is placed perpendicular to the principle axis of a lens is eta times that of the object for a particular position of object on a screen. Without disturbing the position of object and screen, by shifting lens a position can be obtained where the sharp image is 1//eta times that of object. Ratio of difference between the two positions of lens to the focal length of lens is: