Home
Class 12
MATHS
The area (in sq. units) of the region bo...

The area (in sq. units) of the region bounded by the parabola `y=x^2+2" and the lines " y=x+1, x=0 " and " x=3`, is

A

`(15)/(4)`

B

`(15)/(2)`

C

`(21)/(2)`

D

`(17)/(4)`

Text Solution

Verified by Experts

The correct Answer is:
B
`x^(2)=y-2`
`y=x+1`
For intersection point
`x^2=x+1-2`
`x^2-x+1=0`
`D=1-4lt 0`
No intersection point
Area `int_(0)^(3)(x^2+2)dx-int_(0)^(3)(x+1)dx`
`=((x^3)/(3)+2x)_(0)^(3)-((x^2)/(2)+x)_(0)^(3)=(9+6)-((9)/(2)+3)=12-(9)/(2)=(15)/(2)`
.
Promotional Banner

Similar Questions

Explore conceptually related problems

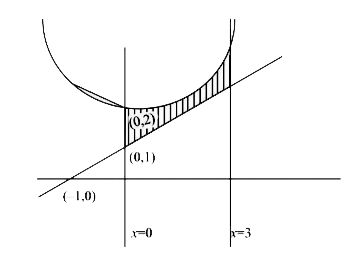
Find the area of the region bounded by: the parabola y=x^(2) and the line y=x

The area (in sq units) of the region bounded by the curve y=sqrt(x) and the lines y=0,y=x-2, is

The area of the region bounded by the parabola y = x^(2) + 2 and the lines y = x, x = 0 and x = 3 is

The area of the region bounded by the parabola y = x^(2) and the line y = 4x is

The area of the region bounded by the parabola x=-y^(2) and the line y=x+2 is

Find the area of the region bounded by the parabola y^(2)=2x and the line x-y=4

Find the area of the region bounded by the parabola y=x^(2) and y=|x|

Find the area of the region bounded by the parabola y=x^(2) and y=|x|

The area of the region bounded by the parabola y ^(2) =9x and the line y = 3x is :