Home
Class 12
MATHS
Find the area of the largest rectangle w...

Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve `y=12-x^2.`

A

`20sqrt(2)`

B

`18sqrt(3)`

C

`32`

D

36

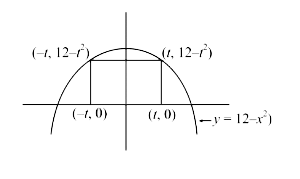
Text Solution

Verified by Experts

The correct Answer is:
C
Area `=A=2t (12-t^2)`
`(d A)/(dt)=24-6t^2`.
For maximum value of `A,(d A)/(dt)=0`
`24-6t^2 =0,t= +- 2`
`A=2t(12-t^2)=32` .
.
Promotional Banner

Similar Questions

Explore conceptually related problems

The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e^(-x^(2) is

The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e^(-x^(2)) is

The maximum area of a rectangle whose two vertices lie on the x-axis and two on the curve y=3-|x|,-3<=x<=3

The area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x - axis and vertices C and D lie on the parabola, y=x^(2)-1 below the x - axis, is :

Maximum area of rectangle whose two vertices lie on the x -axis and two on the curve y=4-|x| quad AA|x|<4 is

Find the area bounded by the curve y=e^(-x) the X-axis and the Y-axis.

Find the area of that region bounded by the curve y="cos"x, X-axis, x=0 and x=pi .

Find the area of the region bounded by the curve y = x^2 , the x-axis, and the lines x = 1 and x = 3.

Find the area between the curves y=x^2 and x=y^2 .