A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
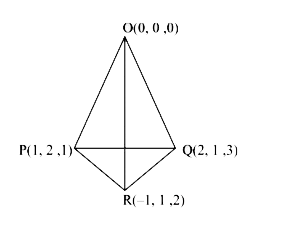
- A tetrahedron has vertices P(1,2,1),Q(2,1,3),R(-1,1,2) and O(0,0,0). T...
Text Solution
|
- एक चतुष्फलक के शीर्ष O ( 0,0,0) , A (1, 2,1) , B(2,1,3) तथा C (...
Text Solution
|
- For any four points O(0,0,0),P(1,2,1),Q(2,3,0),R(0,1,-1), the angle be...
Text Solution
|
- A tetrahedron has vertices P(1,2,1),Q(2,1,3),R(-1,1,2) and O(0,0,0). T...
Text Solution
|
- A tetrahedron has vertices O(0,0,0), A(1,2,1), B(2,1,3) and C(-1,1,2)....
Text Solution
|
- एक चतुश्फलक के चारो शीर्ष O(0,0,0),A(1,2,1),B(2,1,3) और C(-1,1,2) है। ...
Text Solution
|
- एक चतुष्फलक (tetrahedron) के शीर्ष P(1,2,1), Q(2,1,3),R (-1,1,2) तथा O...
Text Solution
|
- एक चतुष्फलक के शीर्ष O(0,0,0),A(1,2,1),B(2,1,3) और C(-1,1,2) हैं, तब फ...
Text Solution
|
- एक चतुष्फलक के शीर्ष O(0,0,0),A(1,2,2),B(2,1,3) तथा C(-1,1,2) हैं , ...
Text Solution
|
 .
.