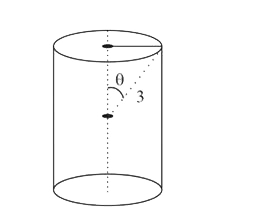
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The height of a right circular cylinder of maxium volume inscirbed in ...
Text Solution
|
- The largest sphere is to be curved out of a right circular cylinder...
Text Solution
|
- The largest sphere is to be curved out of a right circular cylinder...
Text Solution
|
- The height of a right circular cylinder of maxium volume inscirbed in ...
Text Solution
|
- If a right circular cylinder of height 10 is inscribed in a sphere of ...
Text Solution
|
- A right circular cylinder is inscribed in a sphere of radius r. Expr...
Text Solution
|
- The volumes of a sphere and a right circular cylinder having the same ...
Text Solution
|
- The volumes of a sphere and a right circular cylinder havIng the same ...
Text Solution
|
- The largest sphere is to be curved out of a right circular cylinder...
Text Solution
|