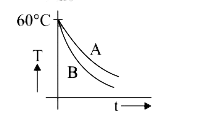
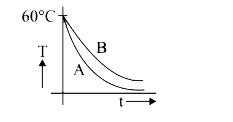
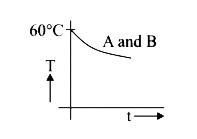
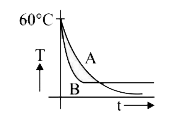
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two identical beakers A and B contain equal volumes of two different l...
Text Solution
|
- A calorimeter of mass 0.2 kg and specific heat 900 J//kg-K . Containin...
Text Solution
|
- The density of a material A is 1500 kg//m^(3) and that of another mate...
Text Solution
|
- Two identical beakers A and B contain equal volumes of two different l...
Text Solution
|
- दो एकसमान बीकर A एवं B में दो भिन्न द्र्वो के समान आयतन 60^(@)C तापमान...
Text Solution
|
- A calorimeter of negligible heat capacity contains 100cc of water at 4...
Text Solution
|
- Two identical beakers A and B contain equal volumes of two different l...
Text Solution
|
- The difference between two specific heats of a gas is 5000 J kg^-1 K^-...
Text Solution
|
- For a gas, the difference between the two specific heats is 41503 Kg^(...
Text Solution
|