Home
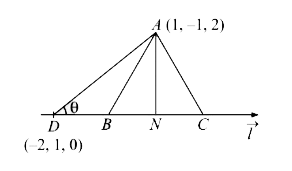
Class 12
MATHS
Let z in C be such that |z| lt 1 .If om...

Let `z in C` be such that `|z| lt 1 `.If `omega =(5+3z)/(5(1-z)` then

A

4 Im `omega gt 5`

B

5 Im `(omega) lt 1`

C

5Re `(omega) gt 4`

D

5 Re `(omega) gt 1`

Text Solution

Verified by Experts

The correct Answer is:
D
`W = (5 + z)/(5(1 - z)), 5w - 5wz = 5 + z`
`z = (5w - 5)/(5w + 3), z = (w - 1)/(w + 3//5)`
`|z| = |(w - 1)/(w + 3//5)| lt 1, |w - 1| lt |w + (3)/(5)|`
Re (w `gt (1)/(5)`, 5 Re (w) `gt` 1
Promotional Banner

Similar Questions

Explore conceptually related problems

If complex number omega=(5+3z)/(5(1-z))|z|<1 then

Let z and omega be two complex numbers such that |z|=1 and (omega-1)/(omega+1) = ((z-1)^2)/(z+1)^2 then value of |omega-1| +|omega+1| is equal to____________

Let z and omega be two complex numbers such that |z|lt=1,|omega|lt=1 and |z-iomega|=|z-i bar omega|=2, then z equals (a)1ori (b). ior-i (c). 1or-1 (d). ior-1

If z_(1) and z_(2) are two complex numbers such that |z_(1)| lt 1 lt |z_(2)| , then prove that |(1- z_(1)barz_(2))//(z_(1)-z_(2))| lt 1

Let z and omega be two complex numbers such that |z|<=1,| omega|<=1 and |z+omega|=|z-1vec omega|=2 Use the result |z|^(2)=zz and |z+omega|<=|z|+| omega|

Suppose z is a complex number such that z ne -1, |z| = 1, and arg(z) = theta . Let omega = (z(1-bar(z)))/(bar(z)(1+z)) , then Re (omega) is equal to

Suppose z is a complex number such that z ne -1, |z| = 1 and arg(z) = theta . Let w = (z(1-bar(z)))/(bar(z)(1+z)) , then Re(w) is equal to