Home
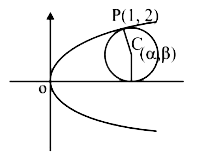
Class 12
MATHS
The area (in sq. units) of the smaller o...

The area (in sq. units) of the smaller of the two circles that touch the parabola, `y^(2) = 4x` at the point (1, 2) and the x-axis is:

A

`4 pi (2 - sqrt(2))`

B

`8 pi (2 - sqrt(2))`

C

`8 pi (3 - 2 sqrt(2))`

D

`4 pi (3 + sqrt(2))`

Text Solution

Verified by Experts

The correct Answer is:
C
`{:(y^(2) = 4x),(2yy' = 4),(y' = (2)/(y)):}|{:(-1 = (beta - 2)/(alpha - 1)),(- alpha + 1 = beta 2),(beta = 3 - alpha):}`
Slope of normal `= (-2)/(2) = - 1`
`(alpha - 1)^(2) + (beta - 2)^(2) = beta^(2)`, `alpha^(2) + beta^(2) - 2alpha = 4 beta +5 = beta^(2)`
`alpha^(2) - 2 alpha - 4 beta + 5 = 0`
`alpha^(2) - 2 alpha - 4 beta + 5 = 0`
`alpha^(2) - 2 alpha - 12 + 4 alpha + 5 = 0`
`alpha^(2) + 2 alpha - 7 = 0`
`(alpha + 1)^(2) = 8`, `alpha + 1 = +- 2 sqrt(2)`
`alpha = - 1 - 2 sqrt(2), -1 + 2 sqrt(2)` `:. beta = 3 - (-1 + 2 sqrt(2))`
Radius `beta = 4 - 2 sqrt(2)`
Area `= pi (beta^(2)) = pi (4 - 2 sqrt(2))^(2) = 4 pi (2 - sqrt(2))^(2) = 4 pi (4 + 2 - 4 sqrt(2)) = 8pi (3 - 2 sqrt(2))`
Promotional Banner

Similar Questions

Explore conceptually related problems

The area ( in sq, units ) of the part of the circle x^2 +y^2 = 36 , which is outside the parabola y^2 = 9x , is

The area (in sq units) in the first quadrant bounded by the parabola, y=x^(2)+1 , the tangent to it at the point (2, 5) and the coordinate axes is

Equation of the smaller circle that touches the circle x^(2)+y^(2)=1 and passes through the point (4,3) is

The equation of the common tangent touching the parabola y^2 = 4x and the circle ( x - 3)^2 +y^2 = 9 above the x-axis is

The area (in sq. units) in the first quadrant bounded by the parabola y=x^2+1 , the tangent to it at the point (2, 5) and the coordinate axes is

The area (in sq. units) bounded by the parabola y=x^2-1 , the tangent at the point (2,3) to it and the y-axis is

Radius of smaller circle that touches the line y=x at (1,1) and also touches the x -axis is:

The area (in sq. units) of the region in the first quadrant bounded by y=x^(2), y=2x+3 and the y - axis is

The area (in sq. units) of the region bounded by the X-axis and the curve y=1-x-6x^(2) is