Home
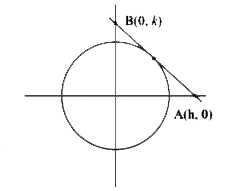
Class 12
MATHS
If a tangent to the circle x^(2)+y^(2)=1...

If a tangent to the circle `x^(2)+y^(2)=1` intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :

A

`x^(2)+y^(2)-2xy=0`

B

`x^(2)+y^(2)-16x^(2)y^(2)=0`

C

`x^(2)+y^(2)-2x^(2)y^(2)=0`

D

`x^(2)+y^(2)-4x^(2)y^(2)=0`

Text Solution

Verified by Experts

The correct Answer is:
D
`rArr` Mid-point `A,B=P=(h/2,k/2)`
`rArr h=2x,k=2y`
Now line as: `x/h+y/x=1` is layout
`rArr (|0/h + 0/k -1|)/(sqrt((1)/(h^(2))+(1)/(k^(2))))=1 rArr (1)/(h^(2))+(1)/(x^(2))=1`
So, locus: `(1)/(4x^(2))+(1)/(4y^(2))=1 rArr x^(2)+y^(2)=4x^(2)y^(2) rArr x^(2)+y^(2)-4x^(2)y^(2)=0`
Promotional Banner

Similar Questions

Explore conceptually related problems

If a tangent to the circle x^(2)+y^(2)=1 intersects the coordinate axes at distinct point P and Q. then the locus of the mid- point of PQ is

If the tangent drawn to the hyperbola 4y^2=x^2+1 intersect the co-ordinate axes at the distinct points A and B, then the locus of the mid-point of AB is:

The tangent at any point P on the circle x^2+y^2=4 meets the coordinate axes at Aa n dB . Then find the locus of the midpoint of A Bdot

if a variable tangent of the circle x^(2)+y^(2)=1 intersects the ellipse x^(2)+2y^(2)=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is

A variable tangent to the circle x^(2)+y^(2)=1 intersects the ellipse (x^(2))/(4)+(y^(2))/(2)=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.

If any tangent to the parabola x^(2)=4y intersects the hyperbola xy=2 at two points P and Q , then the mid point of the line segment PQ lies on a parabola with axs along

If any tangent to the parabola x^(2) = 4y intersects the hyperbola xy = 2 at two points P and Q, then the mid point of line segment PQ lies on a parabola with axis along:

tangent drawn to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 at point 'P' meets the coordinate axes at points A and B respectively.Locus of mid-point of segment AB is

The straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q.If O is the origin and the rectangle OPRQ is completed then the locus of R is