The area (in sq. units) of the region A...

The area (in sq. units) of the region `A={(x,y):x^(2) le y le x+2}` is :

A

`(13)/(6)`

B

`9/2`

C

`(10)/(2)`

D

`(31)/(6)`

Verified by Experts

The correct Answer is:

B

`A={(lambda, 4) , x^(2) le y le x+2}`
`y ge x^(2)` and `y-x-2 le 0`
Point of intersection
`rArr x^(2)=x+2 rArr x^(2)-x -2=0`
`x=-1,2`

`A=[ underset(-1)overset(2)int ((x+2)-x^(2))dx=(x^(2))/(2)+2x-(x^(3))/(3)]_(-1)^(2)=(2+4-8/3)-(1/2-2 +1/3)`
`=8-3-1/2=5-1/2=9/2`

Similar Questions

Explore conceptually related problems

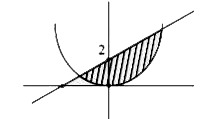
The area (in sq units) of the region A={(x,y):(y^(2))/(2) le x le y+4} is

The area (in sq. units) of the region {(x,y) in R^2: x^2 le y le 3-2x} , is :

If the area (in sq. units) of the region {(x,y):y^(2)le 4x, x+y le 1, x ge 0, y ge 0} is a sqrt(2) +b , then a-b is equal to :

The area ( in sq. units ) of the region A={(x,y):|x| + |y| le 1 , 2y^(2) ge |x|} is :

The area (in sq. units) of the region {(x,y):y^(2) le 2x and x^(2)+y^(2) le 4x , x ge 0, y le 0}, is

The area (in sq units) of the region described by A={(x,y):x^(2)+y^(2) le 1 and y^(2)le 1-x} is :