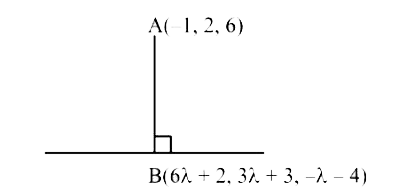A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The distance of the point having position vector -hat(i) + 2hat(j) + 6...
Text Solution
|
- The distance of point B with position vector hat i+2hat j+3hat k from ...
Text Solution
|
- The distance of point B with position vector hat i+2hat j+3hat k from ...
Text Solution
|
- Find the projection of the vector 7 hat i+ hat j-4 hat k in vec a=2 ha...
Text Solution
|
- The length of the perpendicular from the point with position vector ha...
Text Solution
|
- Writhe the projection of the vector 7 hat i+ hat j-4 hat k on the vect...
Text Solution
|
- Find the vector equation of a line passing through the point havi...
Text Solution
|
- The equation of the plane passing through three points A,B,C with pos...
Text Solution
|
- The distance of the point having position vector -hat(i) + 2hat(j) + 6...
Text Solution
|