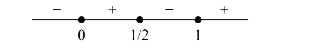A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let f(x) = e^(x)- x and g(x) = x^(2) - x , AA x in R. Then, the set o...
Text Solution
|
- Let R^+ be the set of all non-negative real numbers. If f: R^+\ ->R...
Text Solution
|
- Let f(x) = e^(x) - x and g (x) = x^(2) - x, AA x in R. Then the set of...
Text Solution
|
- Let f(x) = e^(x)- x and g(x) = x^(2) - x , AA x in R. Then, the set o...
Text Solution
|
- Let f:R to R and h:R to R be differentiable functions such that f(x)=x...
Text Solution
|
- माना f(x)=e^(x)-x तथा g(x)=x^(2)-x,AAx inR, तो सभी x inR, जिनके लिए फल...
Text Solution
|
- Let f, g : R rarrR be two functions defined as f(x) = |x| + x and g(x)...
Text Solution
|
- माना f(x) = e^(x) - x तथा g(x) = x^(2) - x, AA x in R, तो सभी x in R ज...
Text Solution
|
- Let f(x)=x^2 \ a n d \ g(x)=sinx for all x in R. Then the set of all ...
Text Solution
|