Home
Class 12
MATHS
If a directrix of a hyperbola centred at...

If a directrix of a hyperbola centred at the origin and passing through the point `(4,-2 sqrt(3)) " is " 5x=4sqrt(5)` and its eccentricity is e, then

Text Solution

Verified by Experts

The correct Answer is:
7

`16/a^(2) -12/b^(2)=1`
`16/a^(2) -12/(a^(2)(e^(2)-1))=1`
`16(e^(2)-1) -12 =a^(2)(e^(2)-1)`, since `a/e =4/sqrt(5)`
`16e^(2) - 16-12 = 16/5 e^(2)(e^(2)-1)`
`80e^(2) - 80 - 60 = 16(e^(4) - e^(2))`
`16e^(4) - 96e^(2) + 140=0`
`4e^(2) - 24e^(2) + 35=0`
Promotional Banner

Similar Questions

Explore conceptually related problems

Equation of the ellipse with centre at origin, passing through the point (-3,1) and e=sqrt((2)/(5)) is

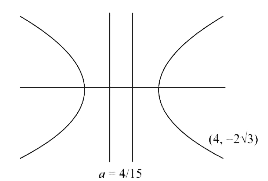
A hyperbola has center at origin and passing through (4-2sqrt(3)) and having directrix 5x=4sqrt(5) then eccentricity of hyperbola (e) satisfy the equation.

A hyperbola, centred at the prigin, has transverse axis 2a. If it passes through a given point ( x_(1), y _(1)), then its eccentricity is

An ellipse passing through the point " (2sqrt(13),4) " has its foci at " (-4,1) " and " (4,1) " .Then its eccentricity is

An ellipse passing through (4sqrt(2),2sqrt(6)) has foi at (-4,0) and (4,0). Then,its eccentricity is

Eccentricity of the hyperbola passing through (3,0) and (3 sqrt(2),2) is

An ellipse passing through the point " (2sqrt(13),4) " .I has its foci at " (-4,1) " and " (4,1) " .Then its eccentricity is

A hyperbola has its centre at the origin, passes through the point (4, 2) and has transverse axis of length 4 along the x-axis. Then the eccentricity of the hyperbola is

Find the equation of hyperbola whose eccentricity = sqrt(2) and passing through (-5,3) .