Home
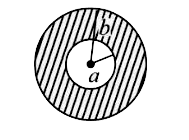
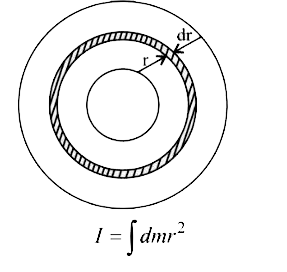
Class 12
PHYSICS
A circular disc of radius b has a hole o...

A circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc varies as `((sigma_(0))/(r))`. then the radius of gyration of the disc about its axis passing through the centre is:

A

`(a+b)/(2)`

B

`sqrt((a^(2)+b^(2)+ab)/(2))`

C

`sqrt((a^(2)+b^(2)+ab)/(3))`

D

`(a+b)/(3)`

Text Solution

Verified by Experts

The correct Answer is:
C

`l=intdmr^(2)`
`rArr" "int_(a)^(d)((sigma_(0))/(r)2pir dr)r^(2)" "rArr" "l=2sigma_(0)pi(b^(3(-a^(3))))/(3)" "rArr" "l=mk^(2)`
`rArr" "2sigma_(0)pi((b^(3)-a^(3)))/(3)=2sigma_(0)pi(b-a)K^(2)" "rArr" "k=sqrt((a^(2)+b^(2)+ab)/(3))`
Promotional Banner

Similar Questions

Explore conceptually related problems

The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is

The radius of gyration of a disc about an axis coinciding with a tangent in its plane is

Calculate the radius of gyration of a circular disc about its diameter.

There is a uniform circular disc of mass 10kg & radius 2 meter. Calculate the radius of gyration if it is rotating about an axis passing through its centre & perpendicular to its plane

A uniform disc (of mass M and radius a ) has a hole (of radius b ) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?

From a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

From a disc of radius R and mass M , a circular hole of diameter R , whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?

A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.