Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
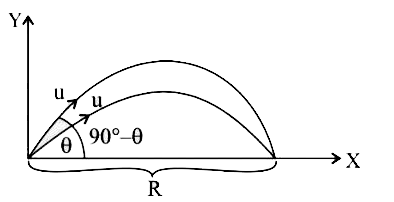
- For a given velocity, a projectile has the same range R for two angles...
Text Solution
|
- Two projectiles are thrown same speed in such a way that their ranges ...
Text Solution
|
- A projectille can have the same range R for two angles of projection. ...
Text Solution
|
- For a given velocity, a projectile has the same range R for two angles...
Text Solution
|
- A projectile has the same range R for two angles of projections but sa...
Text Solution
|
- For a given velocity, a projectile has the same range R for two angles...
Text Solution
|
- A projectile can have the same range R for two angles of projection. I...
Text Solution
|
- A projectile has same range for two angules of projection. If times of...
Text Solution
|
- A projectile has same range R for the two angles of projection. If T(1...
Text Solution
|