Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
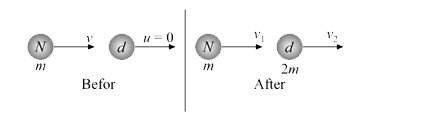
- A neutron makes a head-on elastic collision with a stationary deuteron...
Text Solution
|
- A neutron makes is a head - on elastic collision with a stationary deu...
Text Solution
|
- A neutron collides elastically with an initially stationary deuteron. ...
Text Solution
|
- A neutron collides elastically with an initially stationary deuteron. ...
Text Solution
|
- A neutron moving at a speed v undergoes a head-on elastic collision wi...
Text Solution
|
- It is found that if a neutron suffers an elastic collinear collision w...
Text Solution
|
- एक न्यूट्रॉन किसी स्थिर ड्यूटेरॉन के साथ आमने-सामने टक्कर में आ जाती ह...
Text Solution
|
- A neutron with velocity v suffers head on elastic collision with the n...
Text Solution
|
- A neutron undergoes direct elasticity to a stationary deuteron. The pa...
Text Solution
|