A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
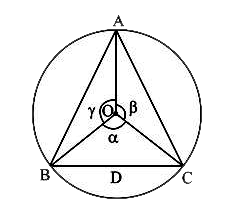
- A triangle is inscribed in a circle. The vertices of the triangle divi...
Text Solution
|
- A circle is inscribed in an equilateral triangle of side a. The area o...
Text Solution
|
- The area of an equilateral triangle,inscribed in a circle is 16V3cm2. ...
Text Solution
|
- A triangle is inscribed in a circle. The vertices of the triangle divi...
Text Solution
|
- A triangle with side lengths in the ration 3:4:5 is inscribed in circl...
Text Solution
|
- एक वृत्त व एक समबाहु त्रिभुज के क्षेत्रफलों में अनुपात जबकि वृत्त का व...
Text Solution
|
- The triangle of maximum area inscribed in a circle is :
Text Solution
|
- A circle is inscribed ina n equilateral triangle and a square is inscr...
Text Solution
|
- A circle is inscribed in an equilateral triangle and a square is inscr...
Text Solution
|