Home
Class 12
MATHS
The area bounded by the curve y = x^2+ 2...

The area bounded by the curve `y = x^2+ 2x + 1,` the tangent at `(1, 4)` and the y-axis is

A

`2/3` sq.unit

B

`1/3` sq.unit

C

2 sq.unit

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
B
Since, `y=x^2 +2x+1 rArr (dy)/(dx)=2x+2 rArr ((dy)/(dx))"|"_(x=1)=2xx1+2=4`
Equation of tangent at (1,4) is y-4=4(x-1)
`rArr` 4x-y=0
`therefore` Required area =`int_0^1ydx-1/2xx1xx4=int_0^1(x^2+2x+1)dx-2=[x^3/3+x^2+x]_0^1 -2=1/3` sq unit
Promotional Banner

Similar Questions

Explore conceptually related problems

The area bounded by the curve y=x^(2) , the normal at (1, 1) and the x-axis is:

The area bounded by the curve y = sin2x, axis and y=1, is

The area of the region bounded by the curve y=x^(3), its tangent at (1,1) and x -axis is

Area bounded by the curves y=x^(2)-1,x+y=3 is

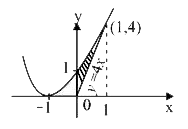
The area bounded by the curve x = 4 - y^(2) and the Y-axis is

The area of the region bounded by the curves y = | x – 2 l, x = 1, x = 3 and the x-axis is

The area bounded by the curve y = x^(2) , X-axis and the lines x = 1, x = 3 is

The area bounded by the curve y=x(x^(2)-1) and x-axis is

Find the area bounded by curve y = x^(2) - 1 and y = 1 .