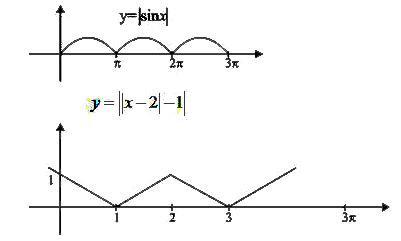A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let f(x)=(sinx)/x and g(x)=|x.f(x)|+||x-2|-1|. Then, in the interval (...
Text Solution
|
- Let g(x)=f(x)+f(1-x) and f^(x)>0AAx in (0,1)dot Find the intervals of ...
Text Solution
|
- Let f(x) be difined in the interval [-2, 2] such that f(x)={{:(-1"...
Text Solution
|
- Let f(x)=(sinx)/x and g(x)=|x.f(x)|+||x-2|-1|. Then, in the interval (...
Text Solution
|
- If f(x)=cosx+sinx and g(x)=x^(2)-1, then g(f(x)) is injective in the i...
Text Solution
|
- If f(x)=((7x+1)sinx)/(e^(x)logx) " and "f^(')(x)=f(x)g(x), then g^(')(...
Text Solution
|
- Let g(x)=f(x)+f(1-x) and f''(x)>0AAx in (0,1)dot Find the intervals of...
Text Solution
|
- agreed f(x)=sinx+cosx,g(x)=x^(2)-1 Then g(f(x)) Will reverse in the fo...
Text Solution
|
- If f(x)=x^2 and g(x)= sinx thenf@g(x) is
Text Solution
|