A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
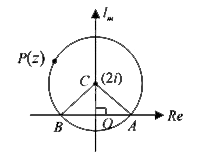
- If 'z, lies on the circle |z-2i|=2sqrt2, then the value of arg((z...
Text Solution
|
- If z ,lies on the circle |z-2i|=2sqrt(2), then the value of arg((z-2)/...
Text Solution
|
- If |z-2i|+|z-2|geq||z|-|z-2-2i||, then locus of z is
Text Solution
|
- If Re ((z + 2i)/(z+4))= 0 then z lies on a circle with centre :
Text Solution
|
- if Im((z+2i)/(z+2))= 0 then z lies on the curve :
Text Solution
|
- The locus of z such that arg[(1-2i)z-2+5i]= (pi)/(4) is a
Text Solution
|
- If "|z-i|=1 &"Arg(z)=(pi)/(2)" then the "z" is (1) "-2i" (2) "0" (4) "...
Text Solution
|
- Let S = {z in C : |z - 2| = |z + 2i| = |z - 2i|} then sum(z in S) |z +...
Text Solution
|
- If z = (1 + 2i)/(1 - (1 -i)^(2)) then find Arg z
Text Solution
|