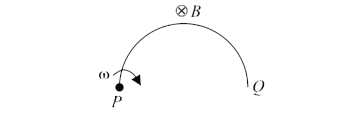
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A wire is bent to form a semi-circle of radius a. The wire rotates ab...
Text Solution
|
- A rod of length l rotates with a small but uniform angular velocity om...
Text Solution
|
- A rod of length l rotates with a uniform angular velocity omega about ...
Text Solution
|
- A wire is in the form of a semicircle of radius r . One end is attache...
Text Solution
|
- a semicircle wire of radius R is rotated with constant angular velocit...
Text Solution
|
- A circular wire of radius r rotates about its own axis with angular sp...
Text Solution
|
- A wire is bent to form a semi-circle of radius a. The wire rotates abo...
Text Solution
|
- A wire is bent to form a semicircle of the radius a. The wire rotates ...
Text Solution
|
- एक तार r त्रिज्या के अर्द्धवृत के रूप में एकसमान चुम्बकीय क्षेत्र B मे...
Text Solution
|