A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let C1 and C2 are circles defined by x^2+y^2 -20x+64=0 and x^2+y^2+...
Text Solution
|
- Let C1 and C2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let...
Text Solution
|
- Let C(1) and C(2) are circles defined by x^(2)+y^(2)-20x+64=0 and x^(2...
Text Solution
|
- Consider the curves C1 : y^2 and C2 : x^2 +y^2-6x+1=0 Assertion (A...
Text Solution
|
- Show that the circle passing through the origin and cutting the circle...
Text Solution
|
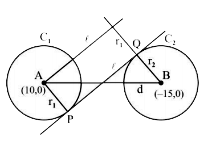
- Two circles C1 and C2 intersect at two distinct points PandQ in a line...
Text Solution
|
- Let C1 and C2 are circles defined by x^2+y^2 -20x+64=0 and x^2+y^2+...
Text Solution
|
- Let C1 and C2 are circles defined by x^2+y^2 -20x+64=0 and x^2+y^2+...
Text Solution
|
- Show that the area of the triangle formed by the lines y=m1x+c1,""...
Text Solution
|