Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
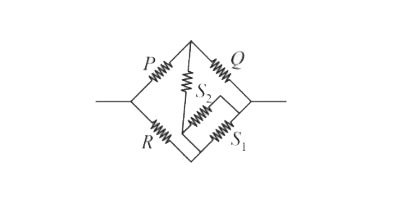
- In a Wheatstone bridge, three resistance, P, Q and R are connected in ...
Text Solution
|
- In a Wheatstone's bridge, three resistances P,Q and R connected in the...
Text Solution
|
- व्हीटस्टोन सेतु की तीन भुजाओ में P,Q और R जुड़े है और S(1)तथा S(2) दो...
Text Solution
|
- यदि P,Q,R व स व्हीटस्टोन सेतु की भुजाओ के प्रतिरोध हैं तो निम्नलिखित म...
Text Solution
|
- In Wheatstone bridge, the resistances in four arms are 10Omega,10Omega...
Text Solution
|
- The resistance in the first and the second arms of a Wheatstone bridge...
Text Solution
|
- In a wheatstone bridge resistance P , Q , R are connected in the first...
Text Solution
|
- A null point is obtained when two resistors , of resistance r each, ar...
Text Solution
|
- In a Wheatstone bridge, three resistance, P, Q and R are connected in ...
Text Solution
|