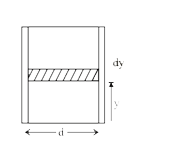
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A parallel plate capacitor has square plates of area A separated by di...
Text Solution
|
- Figure shown a parallel-plate capacitor having square plates of edge ...
Text Solution
|
- A parallel plate capacitor with plate area A & plate separation d is f...
Text Solution
|
- A parallel plate capacitor has plates of area A separated by distance ...
Text Solution
|
- A parallel plate capacitor has square plates of area A separated by di...
Text Solution
|
- The area of the plates of a parallel plate capacitor is A and the gap ...
Text Solution
|
- Find an expression for the capacitance of a parallel plate capacitor w...
Text Solution
|
- A parallel plate capacitor, with plate separation d and plate area A, ...
Text Solution
|
- Figure shown a parallel-plate capacitor having square plates of edge ...
Text Solution
|