A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-MOTION IN TWO AND THREE DIMENSIONS-All Questions
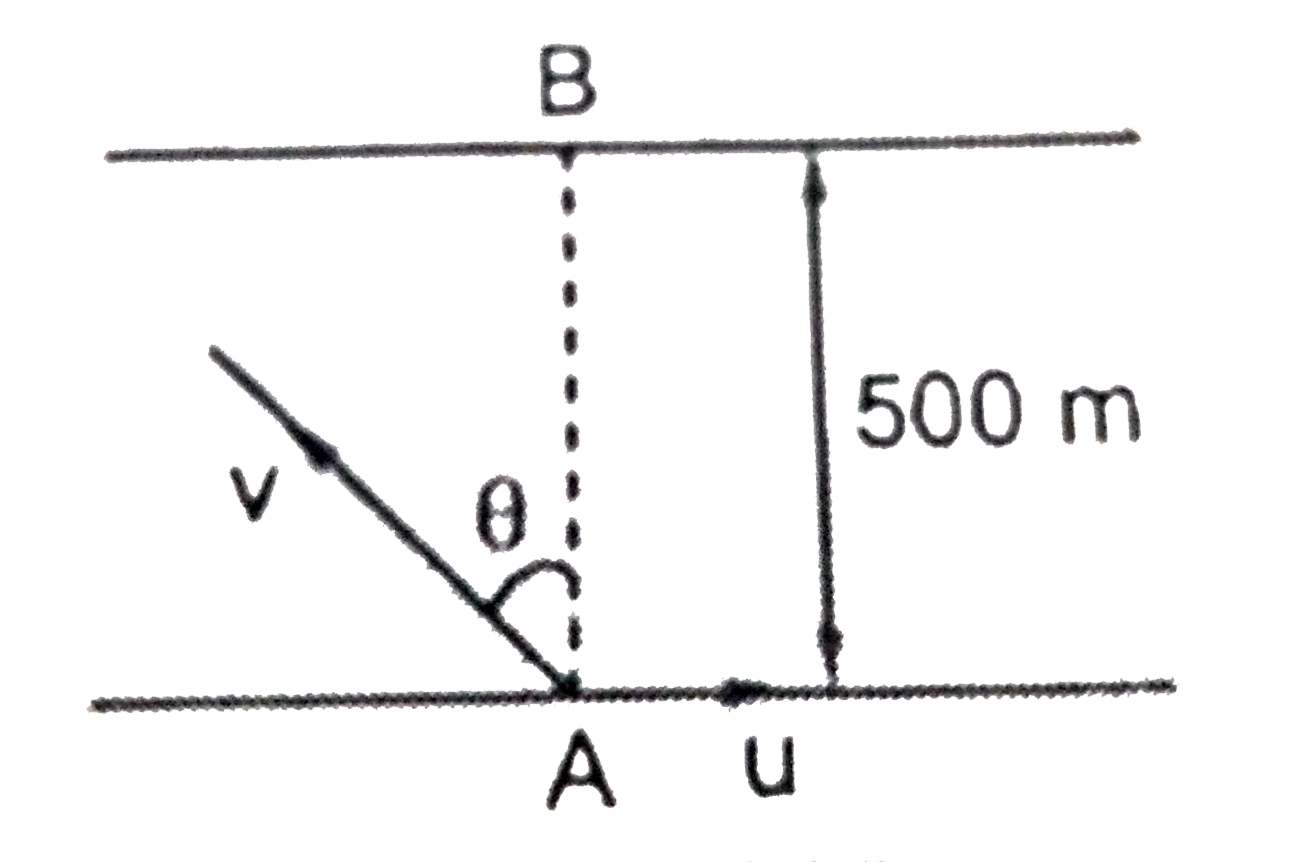
- A swimmer wishes to cross a river 500m width flowing at a rate u. his ...
Text Solution
|
- A particle moves so that its coordinates vary with time as x=alpha sin...
Text Solution
|
- The position of a particle is given as vecr=at hati+bt^(2)hatj Fin...
Text Solution
|
- A ball is projected horizontally in air such that it moves with a cons...
Text Solution
|
- An aeroplane is flying at a constant height of 1960 m with speed 600 k...
Text Solution
|
- At anchored enemy ship is at a distance 180 sqrt(3) m form the securit...
Text Solution
|
- During volcanic eruption chunks of slid rock are blasted out of the vo...
Text Solution
|
- A gun kept on a striaght horizontal is used to hit a car, traveling al...
Text Solution
|
- A particle is thrown over a triangle from one end of a horizontal base...
Text Solution
|
- A gun is fired from a moving platform and the ranges of theshot are ob...
Text Solution
|
- A rider on an open platform, which is descending at constant speed of ...
Text Solution
|
- A block of ice starts sliding down from the top of the inclined roof o...
Text Solution
|
- A stone is projected at an angle alpha to the horizontal from the top ...
Text Solution
|
- A jet plane files horizonally at a height h at a speed v. An anti-airc...
Text Solution
|
- A man standing on a hill top projects a stone horizontally with speed ...
Text Solution
|
- Two inclined planes OA and OB having inclinations 30^@ and 60^@ with t...
Text Solution
|
- A man can row a boat with 4km/h in still water, if he is crossing a ri...
Text Solution
|
- Two swimmers start at the same time from point A one bank of a river t...
Text Solution
|
- An aircraft flies at 400 km//h in still air. A wind of 200sqrt2 km//h ...
Text Solution
|
- To a man walking at the rate of 3 km//h the rain appear to fall vetica...
Text Solution
|
- Three insects A,B and C are situated at the vertices of an equillatera...
Text Solution
|