लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
गाउस का नियम एव इसके अनुप्रयोग
SANJEEV PUBLICATION|Exercise वस्तुनिष्ठ प्रश्न-|26 Videosगाउस का नियम एव इसके अनुप्रयोग
SANJEEV PUBLICATION|Exercise अतिलघुत्तरात्मक प्रश्न-|19 Videosकिरण प्रकाशिकी
SANJEEV PUBLICATION|Exercise अन्य महत्त्वपूर्ण प्रश्न (उच्च स्तरीय बुद्धि-कौशल प्रश्न )-|9 Videosचुम्बकत्व एवं चुम्बकीय पदार्थो के गुण
SANJEEV PUBLICATION|Exercise अन्य महत्त्वपूर्ण प्रश्न(उच्चस्तरीय बुद्धि-कौशल प्रश्न)|27 Videos
SANJEEV PUBLICATION-गाउस का नियम एव इसके अनुप्रयोग -अन्य महत्वपूर्ण प्रश्न (उच्च स्तरीय बुद्धि कौशल प्रश्न )
- काई विघुत क्षेत्र धनात्मक x के लिए धनात्मक x दिशों में एक समान...
Text Solution
|
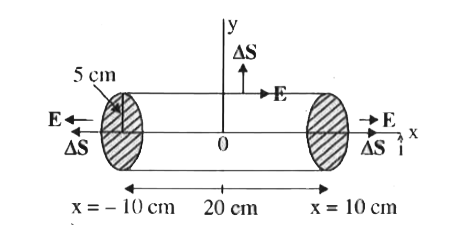
- एक अचालक बेलन एक समान वैधुत क्षेत्र vec(E ) के पूर्णत : भीतर स्थित ...
Text Solution
|
- चित्र में प्रदर्शित गोले S(1) तथा S(2) से गुजरने वाले वैधुत फलक्स ...
Text Solution
|
- Lमीटर भुजा का वर्गीकार पृष्ठ कागज के तल में रखा है। एकसमान वैधु...
Text Solution
|