Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-ELASTICITY AND THERMAL EXPANSION-Exercise - 4 (Level-II)
- Two rods, one of aluminium and other made of steel, having initial len...
Text Solution
|
- A cube of coefficient of linear expansion alpha is floating in a bath ...
Text Solution
|
- A metal of mass 1 kg at constant atmospheric pressure and at initial t...
Text Solution
|
- A 0.1 kg mass is suspended from a wire of negligible mass. The length...
Text Solution
|
- A glass capillary tube is of the shape of a truncated cone with an ape...
Text Solution
|
- Steel wire of length 'L' at 40^@C is suspended from the ceiling and th...
Text Solution
|
- One end of a horizontal thick copper wire of length 2L and radius 2R i...
Text Solution
|
- In plotting stress versus strain curves for two material P and Q, a st...
Text Solution
|
- The ends Q and R of two thin wires, PQ and RS, are soldered (joined) t...
Text Solution
|
- A steel wire of diameter 0.5 and Young’s modulus 210 carries a load o...
Text Solution
|
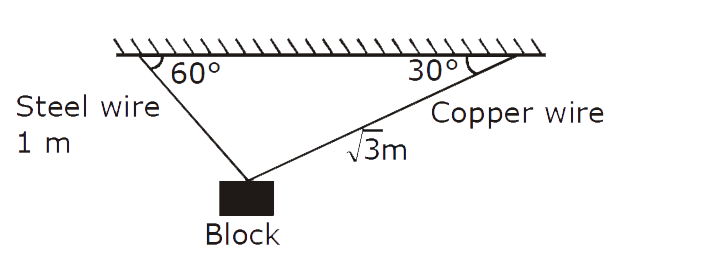
- A block of weight 100 N is suspended by copper and steel wires of same...
Text Solution
|