Home
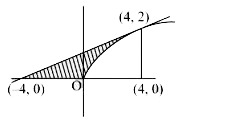
Class 12
MATHS
The area (in square units) of the region...

The area (in square units) of the region bounded by `y = sqrt(x), x ge 0` tangent to it at `(4,2)` & x-axis is :

A

`16/3`

B

`2/3`

C

`8/3`

D

`32/3`

Text Solution

Verified by Experts

The correct Answer is:
C
`(dy)/(dx) = 1/(2sqrt(x)) = 1/4 at (4/2)`
Equation of tangent is `x - 4y + 4 = 0`
shaded area = `1/2 xx 8 xx 2 - int_(0)^(4) sqrt(x) dx = 8 - |2/3 x^(3//2)|_(0)^(4) = 8 - 2/3 codt 4.2 = 8/3` square units.
Promotional Banner

Similar Questions

Explore conceptually related problems

The area (in square units) of the region bounded by y^(2)=2x and y=4x-1 , is

The area (in sq units) of the region bounded by the curve y=sqrt(x) and the lines y=0,y=x-2, is

The area (in square units) of the region described by {(x, y):y^(2)le 2x and y le 4-x} is

Area (in square units) of the region bounded by the curve y^(2)=4x, y-axis and the line y=3 , is

If Delta be the area in square units of the region bounded by the parabola y=-x^2-2x+3 , the line tangent to it at the point P(2,-5) and the y-axis, then 3Delta is equal to…

The area in square units of the region bounded by the curve x^(2)=4y , the line x=2 and the x-axis, is

The area (in square units) of the region bounded by the curves y+2x^(2)=0, y+3x^(2)=1 is equal to