Home
Class 12
PHYSICS
A non uniform rod OM (of length l m) is ...


A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to `lamda=lamda_(0)((x^(3))/(L^(3)))`
Where unit of `lamda_(0)` is kg/m. What is the value of x so that moment of inertia of rod about axis AB `(I_(AB))` is minimum?

A

`(7l)/(15)`

B

`(2l)/(5)`

C

`(81)/(15)`

D

`(4l)/(5)`

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • JEE MOCK TEST 13

    NTA MOCK TESTS|Exercise PHYSICS|25 Videos

  • JEE MOCK TEST 15

    NTA MOCK TESTS|Exercise MCQS (PHYSICS)|25 Videos

Similar Questions

Explore conceptually related problems

A rod length L and mass M is placed along the x -axis with one end at the origin, as shown in the figure above. The rod has linear mass density lamda=(2M)/(L^(2))x, where x is the distance from the origin. Which of the following gives the x -coordinate of the rod's center of mass?

A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is

A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :

Linear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as lambda = lambda_0 x^3 ( lamda_0 is positive constant). Distance of centre of mass the rod, form end B is

The moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is

A non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is lambda = lambda_(0)x . The centre of mass of rod divides the length of the rod in the ratio:

Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.

The linear mass density of a thin rod AB of length L varies from A to B as lambda (x) =lambda_0 (1 + x/L) . Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :

NTA MOCK TESTS-JEE MOCK TEST 14-PHYSICS
  1. A satellite is revolving in a circular orbit at a height h from the ea...

    Text Solution

    |

  2. An ideal monatomic gas is confined in a cylinder by a spring-loaded pi...

    Text Solution

    |

  3. Two magnetic dipoles X and Y are kept at a distance d apart, with thei...

    Text Solution

    |

  4. Three blocks are suspended as shown in the figure. The acceleration of...

    Text Solution

    |

  5. The rate of disintegration of a radioactive substance falls from (40)/...

    Text Solution

    |

  6. A body executes simple harmonic motion under the action of a force F1 ...

    Text Solution

    |

  7. In a photoelectric experiment, the wavelength of the light incident on...

    Text Solution

    |

  8. A vessel contains oil (density =0.8gm//cm^3) over mercury (density =13...

    Text Solution

    |

  9. A glass prism is immeresed in water as shown in the figure. When a bea...

    Text Solution

    |

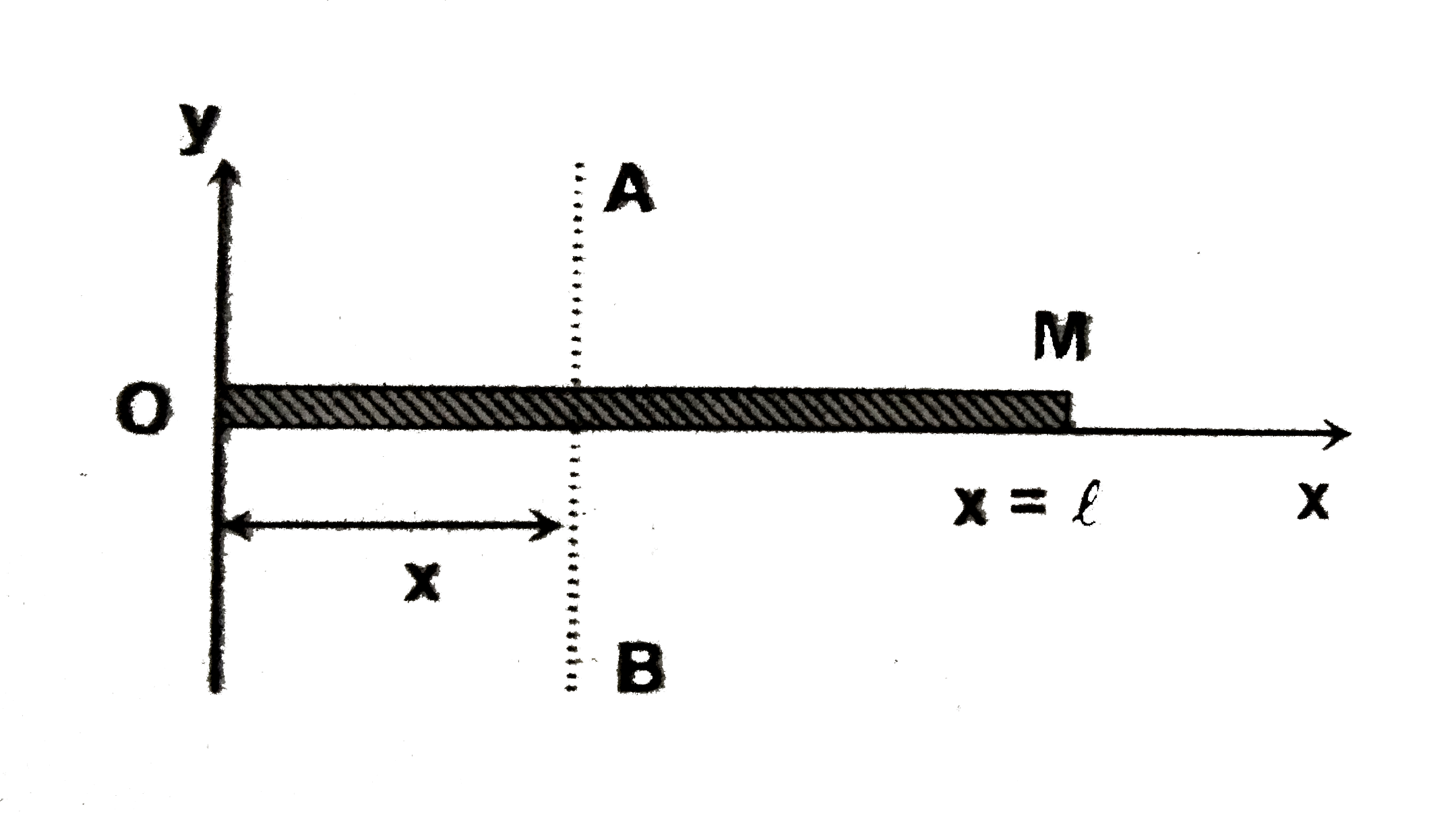
  10. A non uniform rod OM (of length l m) is kept along x-axis and rotating...

    Text Solution

    |

  11. For a CE transistor amplifier, the audio signal voltage across the col...

    Text Solution

    |

  12. A cylindrical adiabatic container of total volume 2V(0) divided into t...

    Text Solution

    |

  13. If velocity, force and time are taken as the fundamental quantities, t...

    Text Solution

    |

  14. Width of the principal maximum on a screen at a distance of 50 cm from...

    Text Solution

    |

  15. two particle of medium disturbed by the wave propagation are at x(1)=0...

    Text Solution

    |

  16. The value of the resistance of a carbon resistor having the standard c...

    Text Solution

    |

  17. A conducing circular loop of area 2.5xx10^(-3)m^(2) and resistance 10O...

    Text Solution

    |

  18. An infinitely long solid cylinder of radius R with uniform volume char...

    Text Solution

    |

  19. A stone of mass 1.3 kg is being rotated in a horizontal plane as a con...

    Text Solution

    |

  20. Three travelling waves are superimposed. The equations of the wave are...

    Text Solution

    |