Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-AREA UNDER THE CURVE-EXERCISE -3
- For what value of 'a' is the area bounded by the curve y=a^2x^2 +ax+...
Text Solution
|
- Consider the collection of all curve of the form y = a – bx^(2) that p...
Text Solution
|
- For the curve f(x) = 1/(1+x^(2) , let two points on it are A(alpha, f(...
Text Solution
|
- Let ‘c’ be the constant number such that c gt 1. If the least area ...
Text Solution
|
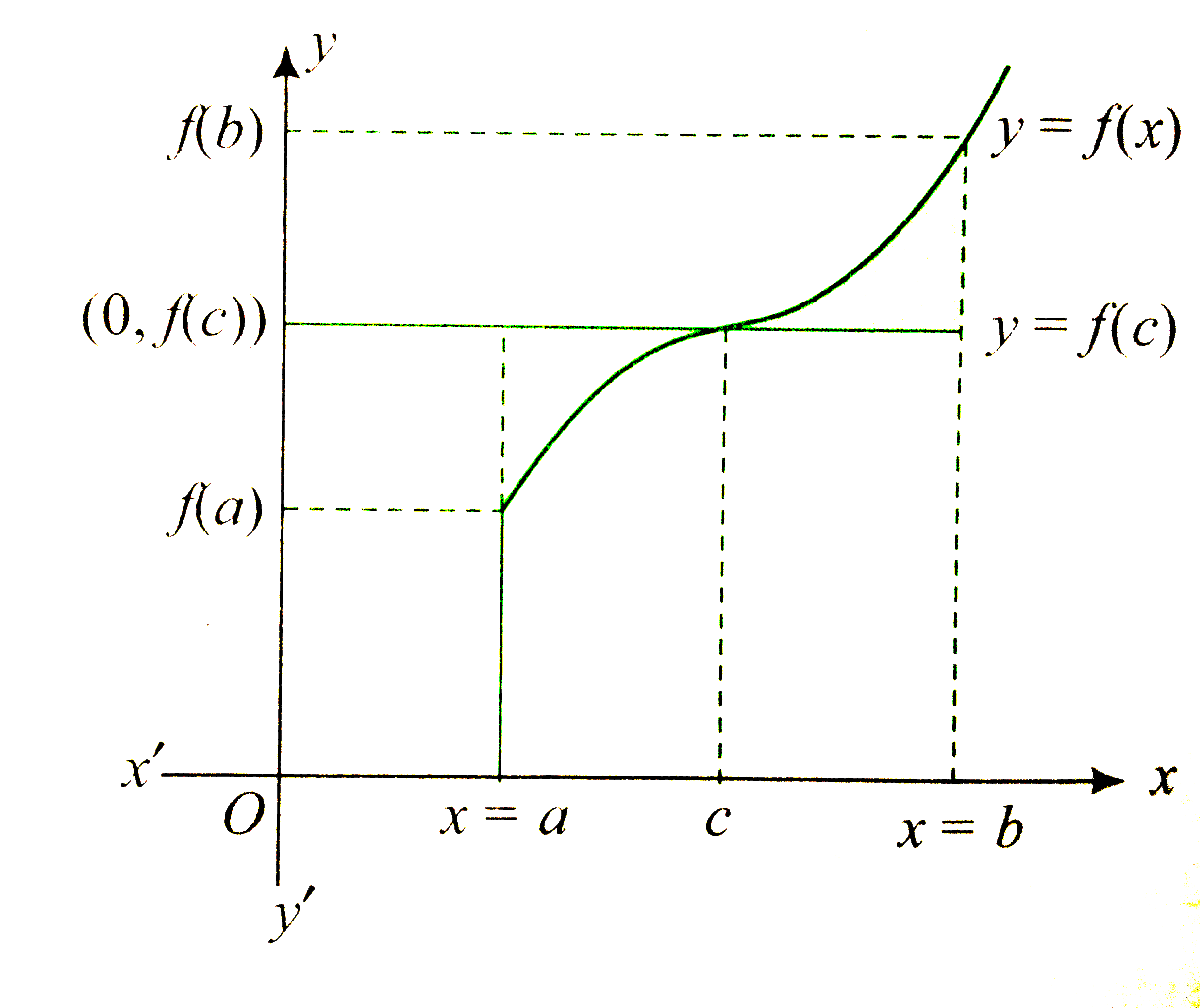
- If y=f(x) is a monotonic function in (a,b), then the area bounded by t...
Text Solution
|
- For what values of a in [0, 1] does the area of the fiqure bounded by ...
Text Solution
|
- A figure is bounded by the curves y =|sqrt2 sin((pix)/4)|,y=0, x=2&x=4...
Text Solution
|
- The line 3x +2y=13 divides the area enclosed by the curve, 9x^2+4y^2-1...
Text Solution
|
- Find the area bounded by the curve y = xe^(-x^2) , the x-axis, and the...
Text Solution
|
- A polynomial function f(x) satisfies the condition f(x+1)=f(x) + 2x + ...
Text Solution
|
- Find the equation of the line passing through the origin and dividing ...
Text Solution
|
- Consider the curve y=x^n where n > 1 in the 1^st quadrant. Ifthe areab...
Text Solution
|
- In the adjacent figure the graph of two function y=f(x) and y=sin x ar...
Text Solution
|
- If An be the area bounded by the curve y=(tanx^n) ands the lines x=0,\...
Text Solution
|
- Find the whole area included between the curve x^2)y^(2) = a^(2)(y^(2)...
Text Solution
|
- Let C(1 )and C(2) be two curves passing through the origin as shown in...
Text Solution
|
- Consider the two curves y = 1//x^(2) and y = 1//[4(x-1)]. At what v...
Text Solution
|
- If A = [[ln(a-1),0],[0,ln(b-1)]], then A^(-1) is :
Text Solution
|
- If z is a complex number such that z = ln(a – 1) + iln (b – 1) then ar...
Text Solution
|
- {:(,"Column - I", "Column - II"),("(A)" ,"The area bounded by curve","...
Text Solution
|