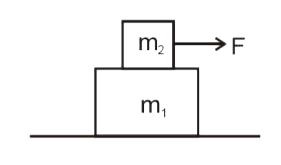
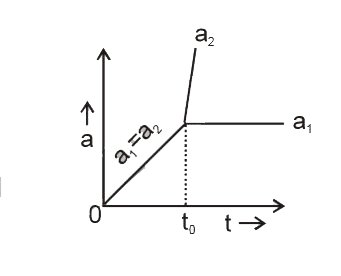
Text Solution
Verified by Experts
Topper's Solved these Questions
NLM & FRICTION
MOTION|Exercise EXERCIS-1|80 VideosNLM & FRICTION
MOTION|Exercise EXERCISE-2|66 VideosNLM & FRICTION
MOTION|Exercise EXAMPLE|47 VideosNEWTON'S LAWS OF MOTION & FRICTION
MOTION|Exercise Exercise - 3 Section-B|12 VideosONE DIMENSION MOTION
MOTION|Exercise Exercise - 3 |Section - B Previous Year Problems | JEE MAIN|12 Videos
Similar Questions
Explore conceptually related problems
MOTION-NLM & FRICTION-SOLVED EXAMPLE
- In Fig force F is gradually increased from zero Draw the graph between...
Text Solution
|
- Figure shows two blocks tied by a string. A variable force F =5t is ap...
Text Solution
|
- Figure shows two blocks tied by a string. A variable force F =5t is ap...
Text Solution
|
- Figure shows two blocks tied by a string. A variable force F =5t is ap...
Text Solution
|
- Find the tension in the string in situation as shown in the figure bel...
Text Solution
|
- Two blocks of masses 5kg and 10kg are attached with the help of light ...
Text Solution
|
- Find out the maximum value of F for which both the blocks will move to...
Text Solution
|
- In the above question find the acceleration of both the block when F ...
Text Solution
|
- In the above question find the acceleration of both the block when F ...
Text Solution
|
- Find out the range of force in which both the blocks move together.
Text Solution
|
- FIND MAXIMUM ACCELERATION OF BLOCK A.
Text Solution
|
- Find the accelerations of blocks A and B for the following cases. (A...
Text Solution
|
- What is the minimum acceleration with which bar A (figure) should be s...
Text Solution
|
- Find out the range of force for which smaller block is at rest with re...
Text Solution
|
- The rear side of a truck is open and a box of 40 kg mass is placed 5 m...
Text Solution
|
- Mass m(2) placed on a plank of mass m(1) lying on a smooth horizontal ...
Text Solution
|